SKIVA, Flexible and Modular Side-channel and Fault Countermeasures
Fault attacks [1,2,3,4] consist in physically tampering with a cryptographic device in order to induce faults in its computations. The most common ways to do so consist in under-powering [14] or over-powering [5,11], blasting ionizing light (e.g. lasers) [8,9,12], inducing clock glitches [6,10], or using electromagnetic (EM) impulsions [12,13], or even heating up or cooling down [7], or using X-rays or ion beams [2].
There are several ways to exploit such faults. Algorithm-specific attacks aim at changing the behavior of a cipher at the algorithmic level by modifying either some of its data [27] or alter its control flow by skipping [28] or replacing [10] some instructions. Differential fault analysis (DFA) [15] uses differential cryptanalysis techniques to recover the secret key by comparing correct and faulty ciphertexts produced from the same plaintexts. Safe-error attacks (SEA) [23] simply observes wether a fault has an impact on the output of the cipher, and thus deduce the values of some secret variables. Statistical fault analysis (SFA) [24], unlike SEA and DFA does not require correct (i.e. not faulted) ciphertexts: by injecting a fault at a chosen location and partially decrypting the ciphertext up to that location, SFA can be used to recover secret bits. Innefective fault attacks (IFA) [25] are similar to SEA: the basic idea is to set an intermediate variable at 0 (using a so-called stuck-at-zero fault), and if the ciphertext is unaffected by this fault (the fault is ineffective), this means that the original value of this intermediate variable was already 0, thus revealing secret information. Finally, based on SFA and IFA, SIFA [26] uses ineffective faults to deduce a bias in the distribution of some secret data.
Various countermeasures have been proposed to prevent fault attacks. Hardware protections can either prevent or detect faults, using for instance active or passive shields [30], integrity checks [42] or other tampering detection mechanisms [43,44,45]. However, those techniques tend to be expensive and lack genericity: each countermeasure protects against a known set of attacks and the hardware might still be vulnerable to new attacks [2]. Software countermeasures on the other hand are less expansive and easier to adapt to new attacks. Software countermeasures can be either part of the design of the cryptographic algorithm –in the protocol [31] or the primitive [18]– or applied to implementations of existing ciphers, such as using redundant operations, error detection codes or consistency checks [32,33,34,35].
One must be careful when implementing countermeasures against fault attack, since they can increase the vulnerability to other side-channel analysis [46,19,20]. For instance, [36] shows that using direct redundant bytes leaks more information than using complementary redundant bytes.
Only few work deal with protection against both side-channel analysis and fault injection. Cnudde et al. [48,49] proposed a hardware-oriented approach where redundancy is applied on top of a masked implementation to obtain combined resistance against faults and SCA. Schneider et al. [17] proposed ParTI, which combines threshold implementation (TI) [21] –to defend against SCA– and concurrent error detection [22] –to thwart fault attacks. However, they only target hardware implementations, and the faults they are able to detect are limited in hamming weight. By comparison, CAPA [16] is based on secure multi-party computations protocols (MPC), which allows it to detect more faults than ParTI, but is still hardware-oriented and expensive to adapt to software. Finally, Simon et al. [18] proposed the Frit permutation, which is secure against both faults and SCA by design, and efficient both in hardware and software. However, no solution exist to efficiently secure legacy ciphers at the software level.
SKIVA
SKIVA is a custom 32-bit processor developped by Pantea Kiaei (Virginia Tech) and Patrick Schaumont (Worcester Polytechnic Institute), in collaboration with Karine Heydemann (LIP6), Pierre-Evariste Dagand (LIP6) and myself (LIP6). It enables a modular approach to countermeasure design, giving programmers the flexibility to protect their ciphers against timing-based and power-based side-channel analysis as well as fault injection at various levels of security. Modularity is achieved through bitslicing, each countermeasure being expressed as a transformation from a bitsliced design into another bitsliced design. The capabilities of SKIVA have been demonstrated on the Advanced Encryption Standard, but the proposed techniques can be applied to other ciphers as well.
Usuba provides a SKIVA backend, thus freing the developpers from the burden of writing low-level assembly code to target SKIVA. Furthermore, SKIVA offers 9 different levels of security through 9 combinations of countermeasures: a single Usuba program can be compiled to either.
SKIVA relies on custom hardware instructions to efficiently and securely implement countermeasures against SCA and fault attacks. Those new instructions are integrated on the SPARC V8 instruction set of the open-source LEON3 processor. A patched version of the Leon Bare-C Cross Compilation System’s (BCC) toolchain makes those instructions availabe in assembly and in C (using inline assembly).
We structure the remaining of this post in two parts. First, we present the countermeasures supported by SKIVA and show how they can be combined to offer security against multiple attacks. Then, we conduct a performance evaluation of AES on SKIVA, as well as an experimental evaluation of its tolerance to control faults.
Modular countermeasures
SKIVA supports four protection mechanisms that can be combined in a modular manner: bitslicing to protect against timing attacks, higher-order masking to protect against power side-channel leakage, intra-instruction redundancy to protect against data faults (faults on the data) and temporal redundancy to protect against control faults (faults on the control flow). We use AES as an example, but the techniques are equally applicable to other bitsliced ciphers.
SKIVA requires ciphers to be fully bitsliced. For instance, the 128-bit input of AES is represented with 128 variables. Since each variable stores 32 bits on SKIVA, 32 instances of AES can be computed in a single run of the primitive. The key to compose countermeasures in SKIVA is to use some of those 32 instances to store redundant bits (to protect against fault attacks), or masked shares (to protect against power analysis). The following figure shows the organisation of the slices for masked and intra-instruction-redundant design:
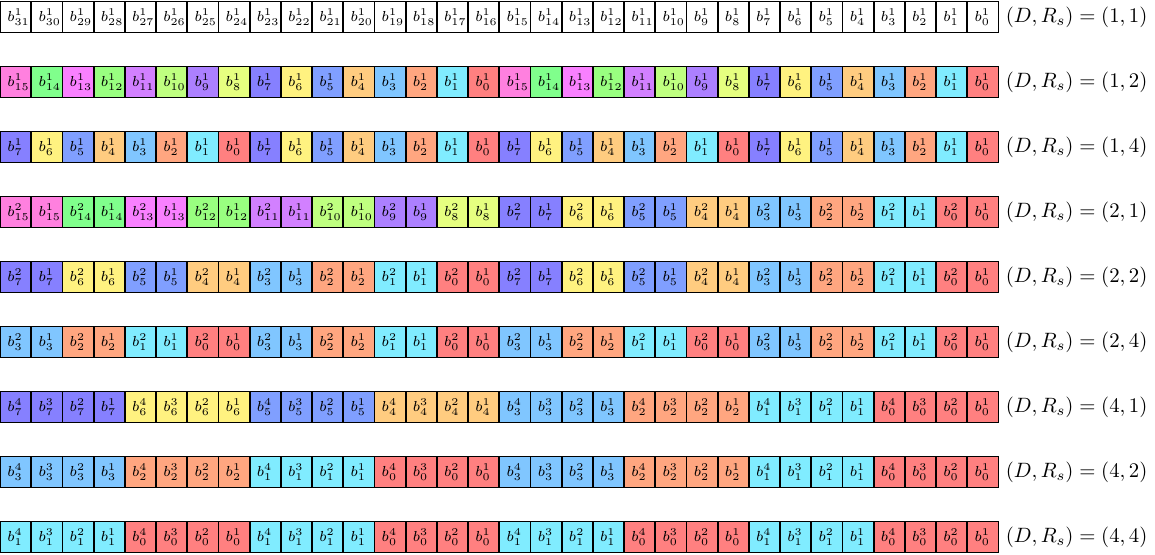
By convention, the letter D is used to denote the number of shares (D ∈ {1,2,4}) of a given implementation. SKIVA supports masking with 1, 2, and 4 shares leading to respectively unmasked, 1st-order, and 3rd-order masked implementations. Within a machine word, the D shares encoding the ith bit are grouped together, as illustrated by the contiguously colored bits bij∈[1,D] in the figure above.
By convention, the letter Rs is used to denote the spatial redundancy (Rs ∈ {1,2,4}) of a given implementation. SKIVA supports spatial redundancy by duplicating a single slice into two or four slices. Within a machine word, the Rs duplicates of the ith bit are interspersed every 32/Rs bits, as illustrated by the alternation of colored words bji∈[1,RS] in the figure above.
Instructions for bitslicing
To efficiently transpose data into their bitslicied representation,
SKIVA offers the instruction tr2 (and invtr2 to perform the
inverse transformation), which interleaves two registers:
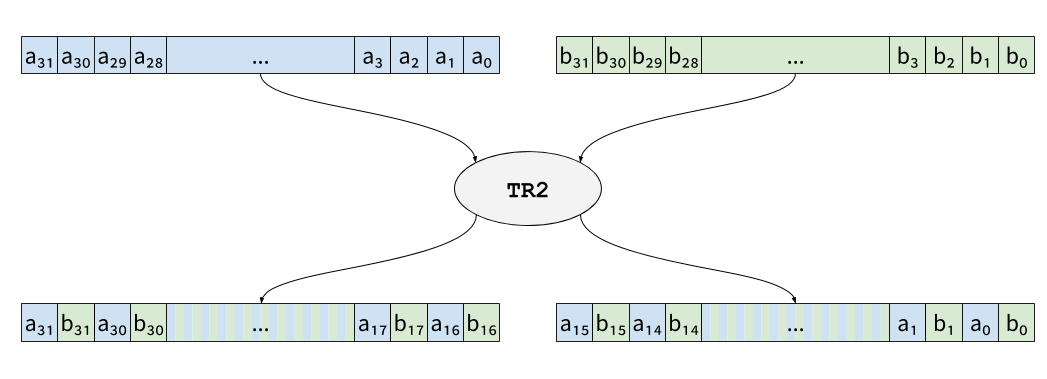
Transposing a n×n matrix can be done using
n×2n-1 tr2 instructions. For instance, transposing
a 4×4 matrix can be done with 4 tr2:
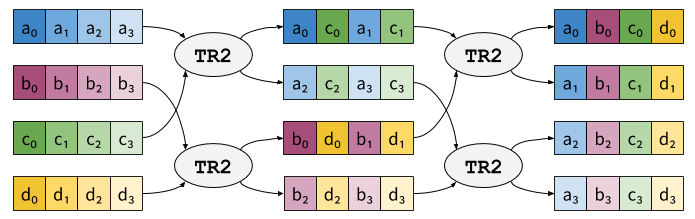
By comparison, transposing the same 4×4 matrix without the tr2
instruction requires 32 operations (as shown in the Bitslicing
post): 8
shifts, 8 ors and 16 ands.
Higher-order Masked Computation
Several masking schemes have been proposed in the litterature, each improving on previous work either by requiring less randomness [53,55], or considering various attacker models [51,52], or providing stronger provable security guarantees [54,29]. Those work are orthonal to SKIVA, which can be seen as a common platform to evaluate masking designs. SKIVA merely offers hardware support to write efficient software implementations of gadgets. Thus, any masking schemes can be used on SKIVA by just providing a software implementation of its gadgets.
To demonstrate SKIVA on AES, we used the NINA gadgets [29], which provide security against both side-channel attacks and faults using the properties of non-interference (NI) and non-accumulation (NA).
In our data representation, the D shares representing any given bit are stored in the same register, as opposed to being stored in D distinct registers. This choice allows a straight-forward composition of masking and redundancy, and is consistent with some previous masked implementations [50].
Instructions for higher-order masking
Computing a masked multiplication between two shared values a and
b requires computing their partial share-products. For instance, if
a and b are represented by two shares
(a0,a1) and
(b0,b1), then the
partial products
a0·b0,
a0·b1,
a1·b0 and
a1·b1 need to be
computed. Since all the shares of a given value are stored in several
slices of the same register, a single and computes n partial
products at once (where n is the number of shares). The shares then
need to be rotated in order to compute the other partial
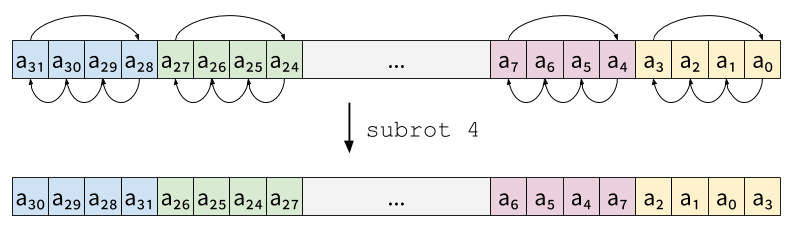
products. SKIVA offers the subrot instruction to perform this
rotation on sub-words. Depending on an immediate parameter, subrot
either rotates two-share slices:
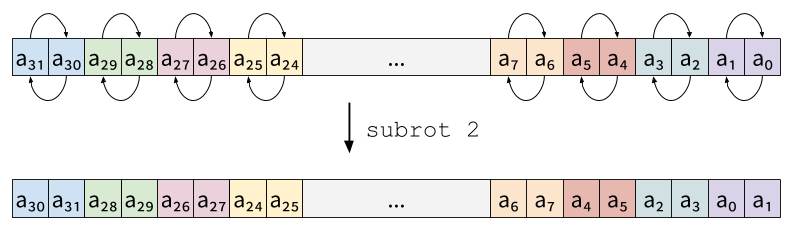
or four-shares slices:
Data-redundant Computation
SKIVA uses intra-instruction redundancy (IIR) [37, 38, 39] to protect implementations against data faults. It supports either a direct redundant implementation, in which the duplicated slices contain the same value, or a complementary redundant implementation, in which the duplicated slices are complemented pairwise. For example, with Rs = 4, there can be four exact copies (direct redundancy) or two exact copies and two complementary copies (complementary redundancy).
In practice, complementary redundancy is favored over direct redundancy. First, it is less likely for complemented bits to flip to consistent values during a single fault injection. For instance, timing faults during state transition [40] or memory accesses [10] follow a random word corruption or a stuck-at-0 model. Second, complementary slices ensure a constant Hamming weight for a slice throughout the computation of a cipher. Futhermore [36] has shown that complementary redundancy results in reduced power leakage compared to direct redundancy.
Instructions for fault redundancy checking and generation
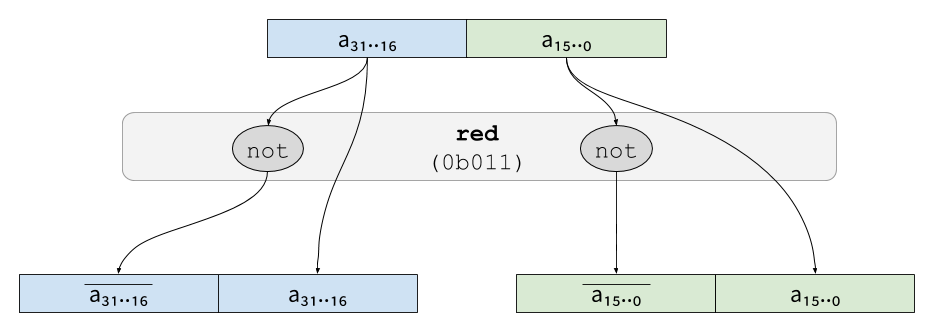
In order to generate redundant bytes to counter fault attacks, SKIVA
provides the red instruction. This instruction can be used to
generate either direct redundancy or complementary redundancy, and
works for both two-shares and four-shares. A immediate passed as
parameter controls which redundancy (direct, complementary, n
shares) is generated. For instance, to generate two-shares
complementary redundant values, the immediate 0b011 would be passed
to red:
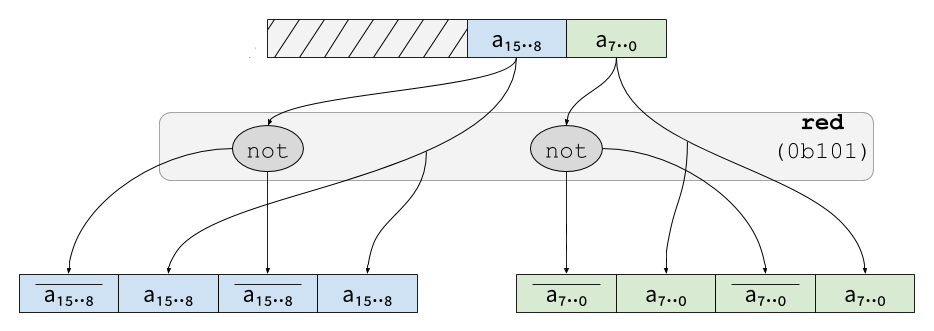
and 0b101 would be used to generate four-shares complementary
redundant values:
The instruction ftchk is used to verify the consistency of redundant
data. In its simplest form, it simply computes the xnor (a xor
followed by a not) of the complementary redundant shares of its
argument. For instance, on a two-shares value:
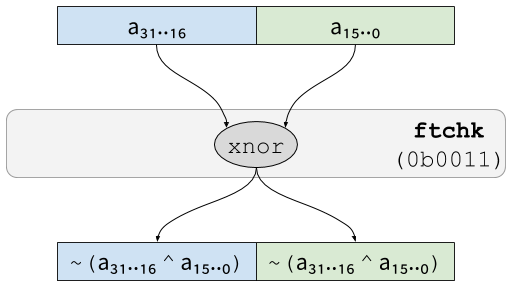
In that case, if the result is anything but 0, then both half of the
input are not (complementary) redundant, which means that a fault was
inserted.
In order to prevent ineffective fault attacks (IFA and SIFA), ftchk
can perform majority-voting on four-shares redundant values. If
complementary redundancy is used, the behavior of ftchk is as
follows:
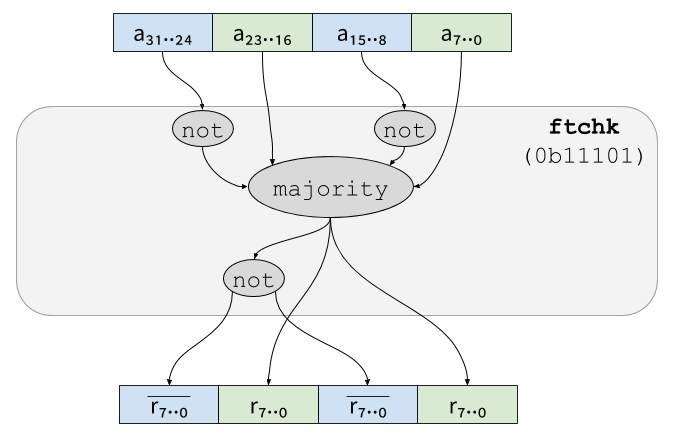
(where majority returns the most common (i.e. majoritary) of its
input).
Instructions for fault-redundant computations
Computations on direct-redundant data can be done using standard
bitwise operations. However, for complementary redundant data, the
bitwise operations have to be adjusted to complement operations. SKIVA
thus offers 6 bitwise instructions to operate of complementary
redundant values. andc16 (resp. xorc16 and xnorc16) performs
and (resp. xor and xnor) on the lower half of its two-shares
redundant arguments, and a nand (resp. xnor and xor) on the
upper half:
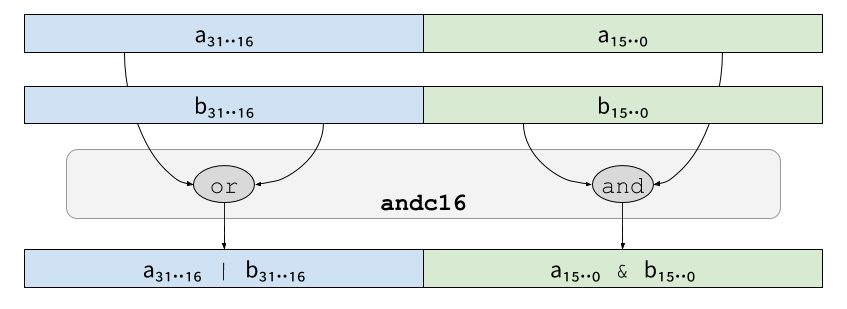
And andc8/xorc8/xnor8 work in the same way on four-shares
redundant values. For instance:
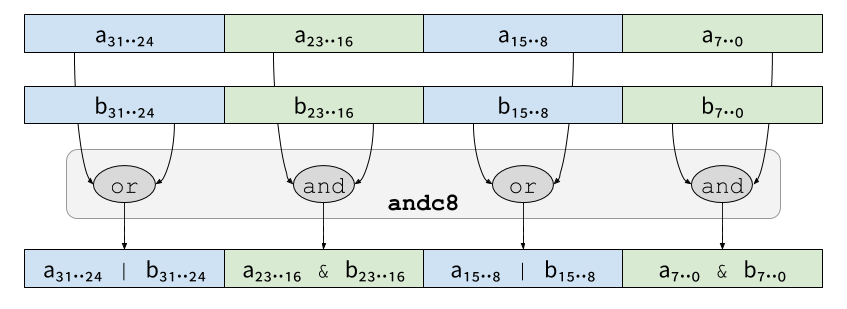
Those operations can be simply written in C as follows, but would take 5 instructions:
#define ANDC8(a,b) (( ((a) | (b)) & 0xFF00FF00) | ( ((a) & (b)) & 0x00FF00FF))
#define XORC8(a,b) ((~((a) ^ (b)) & 0xFF00FF00) | ( ((a) ^ (b)) & 0x00FF00FF))
#define ANDC16(a,b) (( ((a) | (b)) & 0xFFFF0000) | ( ((a) & (b)) & 0x0000FFFF))
#define XORC16(a,b) ((~((a) ^ (b)) & 0xFFFF0000) | ( ((a) ^ (b)) & 0x0000FFFF))
#define XNORC8(a,b) (( ((a) ^ (b)) & 0xFF00FF00) | (~((a) ^ (b)) & 0x00FF00FF))
#define XNORC16(a,b) (( ((a) ^ (b)) & 0xFFFF0000) | (~((a) ^ (b)) & 0x0000FFFF))
Time-redundant Computation
Data-redundant computation does not protect against control faults such as in-struction skip. We, therefore, use a different strategy: we protect our implementation against control faults using temporal redundancy (TR) across rounds [37]. We pipeline the execution of 2 consecutive rounds in 2 aggregated slices. By convention, we use the letter Rt to distinguish implementations with temporal redundancy (Rt = 2) from implementations without (Rt = 1). For Rt = 2, half of the slices compute round i while the other half compute round i − 1. The following figure illustrates the principle of time-redundant bitslicing as applied to AES computation:
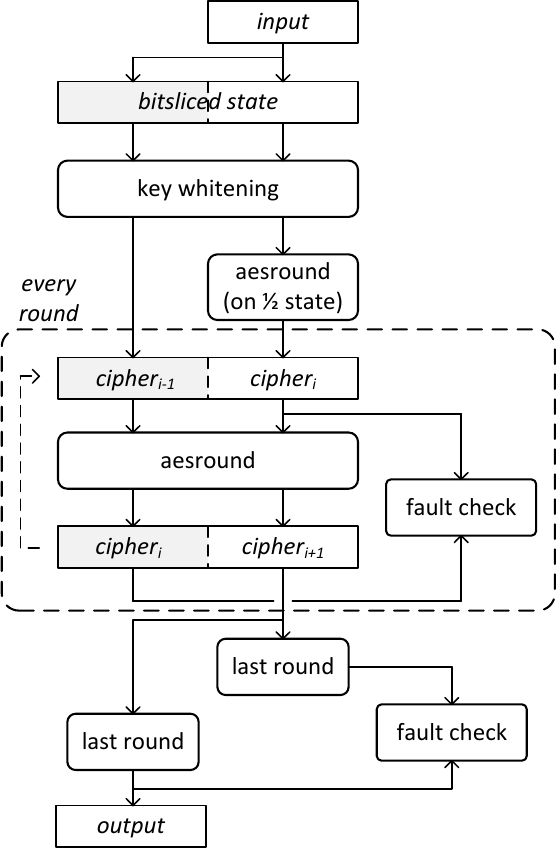
The operation initializes the pipeline by filling half of the slices with the output of the first round of AES, and the other half with the output of the initial key whitening. At the end of round i + 1, we have re-computed the output of round i (at a later time): we can, therefore, compare the two results and detect control faults based on the different results they may have produced. In contrast to typical temporal-redundancy countermeasures such as instruction duplication [40], this technique does not increase code size: the same instructions compute both rounds at the same time. Only the last AES round, which is distinct from regular rounds, must be computed twice in a non-pipelined fashion.
Whereas pipelining protects the inner round function, faults remain possible on the control path of the loop itself. We protect against these threats through standard loop hardening techniques, namely redundant loop counters – packing multiple copies of a counter in a single machine word – and duplication of the loop control structure [41] – producing multiple copies of conditional jumps so as to lower the odds of all of them being skipped through an injected fault.
Results
We used Usubac to generate the 18 different implementations of AES (all combinations of D ∈ {1,2,4}, Rs ∈ {1,2,4} and Rt ∈ {1,2}) for SKIVA. We present a performance evaluation of those 18 implementations, as well as an experimental validation of the security of our control-flow fault countermeasures. For an analysis of the power leakage of those implementations, as well as a theoretical analysis of the security of SKIVA against data faults, we refer to [36].
Performance Evaluation
Our experimental evaluation has been carried on a prototype of SKIVA deployed on the main FPGA (Cyclone IV EP4CE115) of an Altera DE2-115 board. The processor is clocked at 50 MHz and has access to 128 kB of RAM. Our performance results are obtained by running the desired programs on bare metal. We assume that we have access to a TRNG that frequently fills a register with a fresh 32-bit random string. Several implementations of AES are available on our 32-bit, SPARC-derivative processor, with varying degrees of performance. The constant-time, byte-sliced implementation (using only 8 variables to represent 128 bits of data) of BearSSL [39] performs at 48 C/B. Our bitsliced implementation (using 128 variables to represent 128 bits of data) performs favorably at 44 C/B while weighing 8060 bytes: despite significant register pressure (128 live variables for 32 machine registers) introducing spilling and slowing down performance, the rotations of MixColumn and the ShiftRows operations are compiled away, improving performance. This bitsliced implementation serves as our baseline in the following.
Throughput
We evaluate the performance of our 18 variants of AES, for each value of D ∈ {1,2,4}, Rs ∈ {1,2,4} and Rt ∈ {1,2}. To remove the influence of the TRNG’s throughput from the performance evaluation, we assume that its refill frequency is strictly higher than the rate at which our implementation consumes random bits. In practice, a refill rate of 10 cycles for 32 bits is enough to meet this requirement.
| Rₜ = 1 | D | |||
|---|---|---|---|---|
| 1 | 2 | 4 | ||
| Rₛ = 1 | 1 | 44 C/B | 176 C/B | 579 C/B |
| 2 | 89 C/B | 413 C/B | 1298 C/B | |
| 4 | 169 C/B | 819 C/B | 2593 C/B | |
| Rₜ = 2 |
D | |||
|---|---|---|---|---|
| 1 | 2 | 4 | ||
| Rₛ = 1 | 1 | 131 C/B | 465 C/B | 1433 C/B |
| 2 | 269 C/B | 1065 C/B | 3170 C/B | |
| 4 | 529 C/B | 2122 C/B | 6327 C/B | |
For D and Rt fixed, the throughput decreases linearly with Rs. At fixed D, the variant (D, Rs = 1, Rt = 2) (temporal redundancy by a factor 2) exhibits similar performances as (D, Rs = 2, Rt = 1) (spatial redundancy by a factor 2). However, both implementation are not equivalent from a security standpoint. The former offers weaker security guarantees than the latter. Similarly, at fixed D and Rs, we may be tempted to run twice the implementation (D, Rs, Rt = 1) rather than running once the implementation (D, Rs, Rt = 2): once again, the security of the former is reduced compared to the latter since temporal redundancy (Rt = 2) couples the computation of 2 rounds within each instruction, whereas pure instruction redundancy (Rt = 1) does not.
Code size (AES).
We measure the impact of our hardware and software design on code
size, using our bitsliced implementation of AES as a baseline. Our
hardware design provides us with native support for spatial,
complementary redundancy (ANDC, XORC, and XNORC). Performing
these operations through software emulation would result in a ×1.3
(for D = 2) to ×1.4 (for D = 4) increase in code size. One must
nonetheless bear in mind that the security provided by emulation is
not equivalent to the one provided by native support. The temporal
redundancy (Rt = 2) mechanism comes at the expense
of a small increase (less than ×1.06) in code size, due to the loop
hardening protections as well as the checks validating results across
successive rounds. The higher-order masking comes at a reasonable
expense in code size: going from 1 to 2 shares increases code size by
×1.5 whereas going from 2 to 4 shares corresponds to a ×1.6
increase. A fully protected implementation (D = 4,
Rs = 4, Rt = 2) thus weighs 13148
bytes.
Experimental evaluation of temporal redundancy
We simulated the impact of faults on our implementation of AES. We
focus our attention exclusively on control faults (instruction skips)
since we can analytically predict the outcome of data faults [36]. To
this end, we implement a fault injection simulator using gdb running
through the JTAG interface of the FPGA board. We execute our
implementation up to a chosen breakpoint, after which we instruct the
processor to skip the current instruction, hence simulating the effect
of an instruction skip. In particular, we have exhaustively targeted
every instruction of the first and last round as well as the
AES_secure routine (for Rt = 2) and its
counterpart for Rt = 1. Since rounds 2 to 9 use the
same code as the first round, the absence of vulnerabilities against
instruction skips within the latter means that the former is secure
against instruction skip as well. This exposes a total of 1248
injection points for Rt = 2 and 1093 injection
points for Rt = 1. For each such injection point, we
perform an instruction skip from 512 random combinations of key and
plaintext for Rt = 2 and 352 random combinations for
Rt = 1. The results are summarized in the following
table:
| With impact | Without impact | Crash (5) |
# of faults |
|||
|---|---|---|---|---|---|---|
| Detected (1) |
Not detected (2) |
Detected (3) |
Not Detected (4) |
|||
| Rt = 1 | 0.19% | 92.34% | 0.00% | 4.31% | 3.15% | 12840 |
| Rt = 2 | 78.19% | 0.00% | 5.22% | 12.18% | 4.40% | 21160 |
Injecting a fault had one of five effects. A fault may yield an incorrect ciphertext with (1) or without (2) being detected. A fault may yield a correct ciphertext, with (3) or without (4) being detected. Finally, a fault may cause the program or the board to crash (5). According to our attacker model, only outcome (2) witnesses a vulnerability. In every other outcome, the fault either does not produce a faulty ciphertext or is detected within two rounds. For Rt = 2, we verify that every instruction skip was either detected (outcome 1 or 3) or had no effect on the output of the corresponding round (outcome 4) or lead to a crash (outcome 5). Comparatively, with Rt = 1, nearly 95% of the instruction skips lead to an undetected fault impacting the ciphertext. In 0.19% of the cases, the fault actually impacts the fault-detection mechanism itself, thus triggering a false positive.
References
[1] D. Boneh et al., On the Importance of Checking Cryptographic Protocols for Faults, EUROCRYPT, 1997.
[2] H. Bar-El et al., The sorcerer’s apprentice guide to fault attacks, 2004.
[3] Dusko Karaklajic et al., Hardware designer’s guide to fault attacks, 2013.
[4] A. Barenghi et al., Fault Injection Attacks on Cryptographic Devices: Theory, Practice and Countermeasures, 2012.
[5] C. Aumüller et al., Fault Attacks on RSA with CRT: Concrete Results and Practical Countermeasures, CHES, 2002.
[6] R. Anderson, M. Kuhn, Low Cost Attacks on Tamper Resistant Devices, Security Protocols Workshop, 1997.
[7] S. Skorobogatov, Low Temperature Data Remanence in Static RAM, 2002.
[8] S. P. Skorobogatov, R. J. Anderson, Optical Fault Induction Attacks, CHES, 2002.
[9] D. H. Habing, The use of lasers to simulate radiation-induced transients in semiconductor devices and circuits, 1965.
[10] J. Balasch et al., An In-depth and Blackbox Characterization of the Effects of Clock Glitches on 8-bit MCUs, FDTC, 2011.
[11] O. Kömmerling, M. G. Kuhn, Design Principles for Tamper-Resistant Smartcard Processors, Smartcard, 1999.
[12] J.-M. Schmidt, M. Hutter, Optical and EM Fault-Attacks on CRT-based RSA: Concrete Results, 2007.
[13] J.-J. Quisquater, D. Samyde, Eddy current for magnetic analysis with active sensor, Esmart, 2002.
[14] J. J. A. Fournier et al., Security Evaluation of Asynchronous Circuits, CHES, 2003.
[15] E. Biham, A. Shamir, Differential Fault Analysis of Secret Key Cryptosystems, CRYPTO, 1997.
[16] O. Reparaz et al., CAPA: The Spirit of Beaver Against Physical Attacks, CRYPTO, 2018.
[17] T. Schneider et al., ParTI – Towards Combined Hardware Countermeasures against Side-Channel and Fault-Injection Attacks, CRYPTO, 2016.
[18] T. Simon et al., Towards Lightweight Cryptographic Primitives with Built-in Fault-Detection, 2018.
[19] F. Regazzoni et al., Interaction between fault attack countermeasures and the resistance against power analysis attacks, Fault Analysis in Cryptography, 2012.
[20] L. Cojocar et al., Instruction duplication: Leaky and not too fault-tolerant!, CARDIS, 2017.
[21] S. Nikova et al., Threshold Implementations Against Side-Channel Attacks and Glitches, ICICS, 2006.
[22] F. J. MacWilliams, N. J. A. Sloane, The theory of error correcting codes, 1977.
[23] S. M. Yen, M. Joye, Checking Before Output May Not Be Enough Against Fault-Based Cryptanalysis, 2000.
[24] T. Fuhr et al., Fault attacks on AES with faulty ciphertexts only, FDTC, 2013.
[25] C. Clavier, Secret external encodings do not prevent transient fault analysis, CHES, 2007.
[26] C. Dobraunig et al., SIFA: Exploiting Ineffective Fault Inductions on Symmetric Cryptography, 2018.
[27] M. Ciet, M. Joye, Elliptic Curve Cryptosystems in the Presence of Permanent and Transient Faults, Designs, codes and cryptography, 2005.
[28] J.-M. Schmidt, C. Herbst, A Practical Fault Attack on Square and Multiply, FDTC, 2008.
[29] S. Dhooghe, S. Nikova, My Gadget Just Cares For Me - How NINA Can Prove Security Against Combined Attacks, 2019.
[30] O. Kömmerling, M. G. Kuhn, Design Principles for Tamper-Resistant Smartcard Processors, Smartcard, 1999.
[31] M. Medwed et al., Fresh re-keying: Security against Side-Channel and Fault Attacks for Low-Cost Devices, AFRICACRYPT, 2010.
[32] C. Giraud, An RSA Implementation Resistant toFault Attacks and to Simple Power Analysis, 2006.
[33] M. Medwed, J.-M. Schmidt, Coding Schemes for Arithmetic and LogicOperations - How Robust Are They?, WISA, 2009.
[34] R. Karri et al., Concurrent error detection of fault-based side-channel cryptanalysis of 128-bit symmetric block ciphers, DAC, 2001.
[35] G. Gaubatz, B. Sunar, Robust Finite Field Arithmetic forFault-Tolerant Public-Key Cryptography, FDTC, 2006.
[36] P. Kiaei et al., Custom Instruction Support for ModularDefense against Side-channel and Fault Attacks, COSADE, 2020.
[37] C. Patrick et al., Lightweight Fault Attack Resistance in Software Using Intra-instruction Redundancy, SAC, 2016.
[38] B. Lac et al., Thwarting Fault Attacks against Lightweight Cryptography using SIMD Instructions, ISCAS, 2018.
[39] Z. Chen et al., CAMFAS: A Compiler Approach to Mitigate Fault Attacks via Enhanced SIMDization, FDTC, 2017.
[40] L. Zussa et al., Power supply glitch induced faults on FPGA: An in-depth analysis of the injection mechanism, IOLTS, 2013.
[41] K. Heydemann, Sécurité et performance des applications : analyses et optimisations multi-niveaux, 2017.
[42] N. M. Huu et al., Low-cost recovery for the code integrity protection insecure embedded processors, HOST, 2011.
[43] IBM, CCA Basic Services Reference and Guide for the IBM 4758 PCI and IBM 4764 PCI-X Cryptographic Coprocessors, 1997.
[44] S. H. Weingart, Physical Security for the μABYSS System, IEEE Symposium on Security and Privacy, 1987.
[45] D. Chaum, Design concepts for tamper responding systems, Advances in Cryptology, 1984.
[46] F. Regazzoni et al., Power attacks resistance of cryptographic s-boxes with added error detection circuits, DFT, 2007.
[47] Y. Ishai et al., Private Circuits II: Keeping Secrets in Tamperable Circuits, EUROCRYPT, 2006.
[48] T. D. Cnudde, S. Nikova, More Efficient Private Circuits II Through Threshold Implementations, FDTC, 2016.
[49] T. D. Cnudde, S. Nikova, Securing the PRESENT block cipher against combined side-channel analysis and fault attacks, VLSI, 2017.
[50] A. Journault, F.-X. Standaert, Very high order masking: Efficient implementation and security evaluation, CHES, 2017.
[51] G. Barthe et al., Parallel Implementations of Masking Schemes and the Bounded Moment Leakage Model, EUROCRYPT, 2017.
[52] E. Prouff, M. Rivain, Masking against side-channel attacks: A formal security proof, EUROCRYPT, 2013.
[53] M. Rivain, E. Prouff, Provably Secure Higher-Order Masking of AES, CHES, 2010.
[54] G. Barthe et al., Strong Non-Interference and Type-Directed Higher-Order Masking, ACM CCS, 2016.
[55] G. Cassiers, F.-X. Standaert, Towards Globally Optimized Masking: From Low Randomness to Low Noise Rate or Probe Isolating Multiplications with Reduced Randomness and Security against Horizontal Attacks, TCHES, 2019.