Bitslicing

Published on 2020-01-14 by Darius Mercadier

Bitslicing was initially introduced by Biham [1] as an implementation trick to speed up software implementations of the DES cipher. The basic idea of bitslicing is to represent a n-bit data as 1 bit in n distinct registers. On 64-bit registers, there are then 63 unused bits in each register, which can be filled in the same fashion by taking 63 other independent n-bit data, and putting each of their n bits in one of the registers. Bitwise operators on 64-bit (e.g. and, or, xor, not) then act as 64 parallel operators. For instance, bitslicing 3-bit data requires 3 registers. The first bit of each data goes into the first register; the second bit into the second register and the third bit into the third register. Using 4-bit registers (for the sake of simplicity), this can be applied to 4 data:

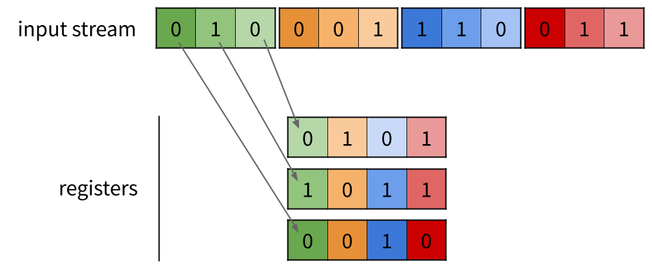
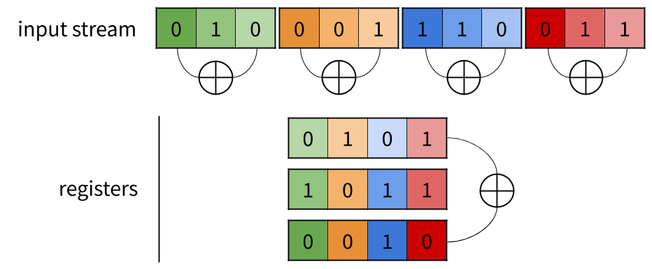
Once the data have this representation, doing a bitwise operation o between two registers actually does m independent o (where m is the size of the registers; 4 in the previous example). For instance, doing a xor between the first and third register above computes 4 xor at a time:

The general idea of bitslicing is thus to transpose m n-bit data into n m-bit registers (or variables). Then, standard m-bit bitwise operations of the CPU can be used and each acts as m parallel operation. Therefore, if a cipher can be expressed as a combination of bitwise operations, it can be ran m times in parallel using bitslicing. A bitsliced program can thus be seen as a parallel circuit (i.e. a composition of logical operations) implemented in software.

In the following, we present various aspects of bitslicing: how to scale bitslice code, how to efficiently compute permutations, how to implement lookup table, why bitslice code is constant time, how to transpose the data, and finally, how bitslicing deals with arithmetic operations.

Scaling

Modern high-end CPUs come with vector instruction sets, also called SIMD (Single Instruction Multiple Data) extensions. The idea of SIMD is to do the same operation on multiple data with a single instruction, thus increasing throughput using data parallelism rather than concurrency. SIMD instructions are made available to C developpers thanks to functions called intrinsics. For instance, the C intrinsics _mm_add_pi8 generates a paddb assembly instruction, which takes 2 64-bit MMX registers, and does 8 8-bit additions on those registers:

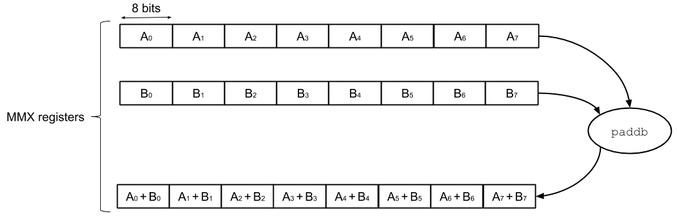
Most non-embedded CPU architectures have SIMD extensions: 128-bit AltiVec on PowerPC, 128-bit Neon on ARM, 64-bit MMX, 128-bit SSE, 256-bit AVX and 512-bit AVX-512 on Intel. While the initial goal of SIMD is to speed up standard computations by providing parallel arithmetic operations, we can use the bitwise operations and large registers they provide to speed up bitsliced implementations. Executing a bitsliced program on 512-bit registers will compute the same circuit on 512 independent data in parallel, thus reducing 8 times the cost per data compared to 64-bit registers. Parallelizing direct (i.e. not bitsliced) code in the same fashion using SIMD instructions is not always possible: a lookup table cannot be parallelized for instance.

The overall time needed to execute the circuit, and thus the latency, on the other hand remains constant no matter the registers used: encrypting 64 inputs in parallel on 64-bit registers, or encrypting 512 inputs int parallel on 512bit registers will take roughly the same amount of time.

Finally, to make full use of SIMD extensions, hundreds of inputs must be available to be encrypted in parallel. For instance, on AES, which encrypts a 128-bit plaintext, in order to fill 512-bit AVX-512 registers, 8 KB of data are required.

Modes of operation

A blockcipher can only encrypt a fixed amount of data, called a block, using between 64 and 128 bits (for instance, 64 for DES, 80 for Rectangle, 128 for AES). When the plaintext is longer than the block size, the cipher must be repeatedly called until the whole plaintext is encrypted, using an algorithm called a mode of operation. The simplest mode of operation is Electronic Codebook (ECB), and consists in dividing the plaintext into sub-plaintexts (of the size of a block), encrypting them separately, and concatenating the resulting sub-ciphertext to produce the full ciphertext:

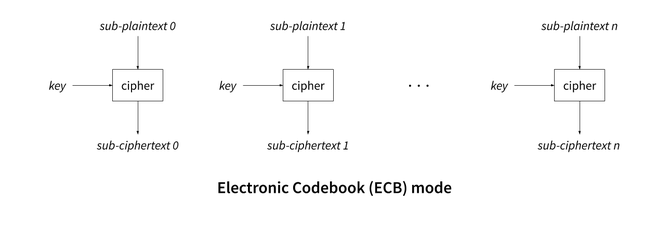
This mode of operation is considered unsecured because identical blocks will be encrypted into the same ciphertext, which can be exploited by an attacker to gain knowledge about the plaintext. For instance, consider the following image:

Encrypting it using AES in ECB mode produces the following image:

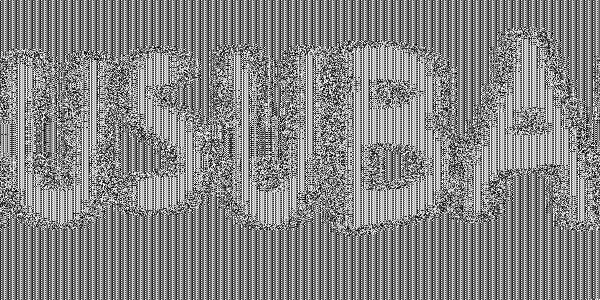
Using a more secure mode instead (namely CTR, presented below) produces the following result:

One of the better, and commonly used mode is Cipher Block Chaining (CBC), which solves the weakness of ECB by xoring each sub-plaintext with the sub-ciphertext produced by the encryption of the previous sub-plaintext. This proccessed is bootstraped by xoring the first sub-plaintext with an additional secret data called an initialization vector:

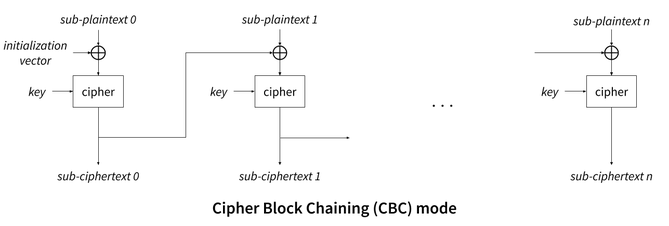
However, because bitslicing encrypts many sub-plaintexts in parallel, it prevents the use of CBC, as well as any other mode that would rely on using a sub-ciphertext as an input for encrypting the next sub-plaintext (like Cipher Feedback (CFB) and Output Feedback (OFB)).

While this reduces the use cases for bitslicing, there are still two ways of overcoming those issues:

In the case of a server encrypting a lot of independent data (coming from different clients), bitslicing can be done in such a way that each parallel data encrypted is independent from the others (i.e. all the data come from different clients). In pratice, it means that to fully exploit n-bit registers, n independent data must be encrypted, which may be hard to obtain in practice. Furthermore, this may incur a slight management overhead.
A parallel mode could be used instead, like Counter mode (CTR). CTR works by encrypting a counter rather than the sub-plaintexts directly, and then xoring the encrypted counter with the sub-plaintext, as shown below:

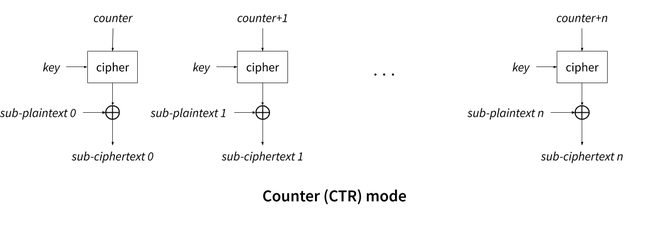
Incrementing the counter can be done in parallel using SIMD instructions:
```
// Load 4 times the initial counter in a 128-bit SSE register
__m128i counters   = _mm_set1_epi32(counter);
// Load a SSE register with integers from 1 to 4
__m128i increments = _mm_set_epi32(1, 2, 3, 4);
// Increment each element of the counters register in parallel
counters = _mm_add_epi32(counters, increments);
// |counters| can now be transposed and encrypted in parallel
```
CTR can thus be fully parallelized and therefore allows bitslicing to encrypt a lot of data from a single origin in parralel.

Compile-time permutations

One of the important properties of any cipher is diffusion: it ensures that if 2 plaintexts differ by 1 bit, then statistically half of the bits of the corresponding ciphertexts should differ. In practice, this property is often achieved using permutations. For instance, Piccolo [2] uses the following 8-bit permutation:

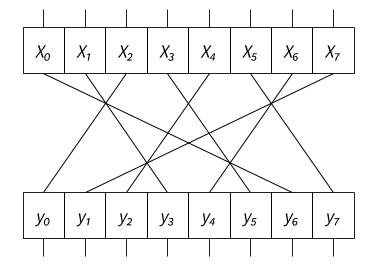
A naive non-bitsliced C implementation would be:

char permut(char x) {
    return ((x & 128) >> 6) |
           ((x & 64)  >> 2) |
           ((x & 32)  << 2) |
           ((x & 16)  >> 2) |
           ((x & 8)   << 2) |
           ((x & 4)   >> 2) |
           ((x & 2)   << 2) |
           ((x & 1)   << 6);
}

A clever developper (or a smart compiler) could notice that the three right-shifts by 2 can be merged together: ((x & 64) >> 2) | ((x & 16) >> 2) | ((x & 4) >> 2) can be optimized to (x & (64 | 16 | 4)) >> 2. The same goes for the three left-shifts by 2, and the permutation can therefore be written as (with the masks written in binary for more simplicity):

char permut(char x) {
    return ((x & 0b10000000) >> 6) |
           ((x & 0b01010100) >> 2) |
           ((x & 0b00101010) << 2) |
           ((x & 0b00000001) << 6);
}

Bitslicing allows to do even better: this permutation would be written as simply 8 assignments in a bitsliced code:

void permut(bool x0, bool x1, bool x2, bool x3,
            bool x4, bool x5, bool x6, bool x7,
            bool* y0, bool* y1, bool* y2, bool* y3, 
            bool* y4, bool* y5, bool* y6, bool* y7) {
    *y0 = x2;
    *y1 = x7;
    *y2 = x4;
    *y3 = x1;
    *y4 = x6;
    *y5 = x3;
    *y6 = x0;
    *y7 = x5;
}

The C compiler can then inline this function, and get rid of the assigments by doing copy propagation, thus effectively performing this permutation at compile time. This technique can be applied to any bit-permutation, as well as to shifts and rotations, making them effectively free (i.e. done at compile time) in bitslicing.

Lookup tables

The other important property of ciphers is confusion, which means that each bit of a ciphertext should depend on several bits of the encryption key in order to obscure the relationship between the two. Most ciphers achieve this property using functions called Sbox (for Substitution-box), often defined using lookup tables. Such tables cannot be used in bitslicing, since each bit of the index would be in a different register. Instead, equivalent circuits can be used, as illustrated in post 1: Usuba - the genesis. As a larger example, we can take Rectangle’s lookup table [6], defined as:

char table[16] = { 
    6 , 5, 12, 10, 1, 14, 7, 9,
    11, 0, 3 , 13, 8, 15, 4, 2
};

It’s a 4x4 lookup table: you need 4 bits to index its 16 elements, and it returns integers on 4 bits (0 to 15). An equivalent circuit to this table is:

void table(bool  a0, bool  a1, bool  a2, bool  a3,
           bool* b0, bool* b1, bool* b2, bool* b3) {
    bool t1  = ~a1;
    bool t2  = a0 & t1;
    bool t3  = a2 ^ a3;
    *b0      = t2 ^ t3;
    bool t5  = a3 | t1;
    bool t6  = a0 ^ t5;
    *b1      = a2 ^ t6;
    bool t8  = a1 ^ a2;
    bool t9  = t3 & t6;
    *b3      = t8 ^ t9;
    bool t11 = *b0 | t8;
    *b2      = t6 ^ t11;
}

Using the principle of bitslicing, we can use 64-bit variables (uint64_t in C) instead of bool, thus computing the Sbox 64 times in parallel. Bitslicing can thus provide a speedup compared to direct code: accessing to a data in the original table will take about 1 cycle (assuming a cache hit), while doing the 12 instructions from the circuit above should take 12 cycles or less to compute 64 times the Sbox (on 64-bit registers), thus costing at most 0.19 cycles per Sbox.

Converting a lookup table into a circuit can be easily done using Karnaugh maps or Binary decision diagrams. However, this would produce large circuits, containing much more instructions than minimal circuits would. Brute-forcing every possible is unlikely to yield any results, as even a small 4x4 Sbox requires usually a circuit of about 12 instructions, and hundreds of billions of such circuits exist. Heuristic can be added to the brute-force search in order to reduce the complexity of the search [7], but this doesn’t scale well beyond 4x4 Sboxes. For larger Sboxes, like AES’s 8x8 Sbox, cryptographers often have to analyze the Sboxes’ underlying mathematical structure to optimize them, which becomes a tedious and highly specialized job [9, 10]. Unfortunately, such a task is hard to automatize, and is unavoidable to obtain good performances from bitslicing a cipher with large Sboxes.

Constant-time

Bitslicing prevents from branching on secret data, since within each register, each bit represents a different data. In particular, the branch condition could be, at the same time, true for some data, and false for others. Thus, both branches of conditionals need to be computed, and combined by masking with the branch condition. For instance, the following branching code (assuming x, a, b, c and d are all booleans, for the sake of simplicity):

if (x) {
    a = b;
} else {
    a = c ^ d;
}

would be implemented in a bitsliced code as:

a = (x & b) | (~x & (c ^ d));

If x is a secret data, the branching code is vulnerable to timing attacks: it runs faster if x is true than if it’s false. An attacker could thus observe the timing execution and deduce the value of x. On the other hand, the bitsliced code executes the same instructions no matter the value of x and is thus immune to timining attacks. For large conditionals, this would come at a cost expanse, since computing both branches is more expensive than computing a single one. However, this is usually not an issue, since most cryptographic primitives avoid using large conditionals.

The lack of branches is not enough to make a program constant-time: memory accesses at secret indices could be vulnerable to cache-timing attacks (presented in the post 1: Usuba - the genesis). However, as shown in the previous section, bitslicing prevents such memory accesses by replacing lookup tables by constant-time circuits. Bitsliced codes are thus constant-time by construction.

Transposition

Transposing the data from a direct representation to a bitsliced one is expensive. Naively, this would be done bit by bit, with the following algorithm for a matrix of 64 64-bit registers (a similar algorithm can be used for any matrix size):

void naive_transposition(uint64_t data[64]) {
    // transposing |data| in a local array
    uint64_t transposed_data[64] = { 0 };
    for (int i = 0; i < 64; i++) {
        for (int j = 0; j < 64; j++) {
            transposed_data[j] |= ((data[i] >> j) & 1) << i;
        }
    }
    // copying the local array into |data|, thus transposing |data| in-place
    memcpy(data, transposed_data, 64 * sizeof(uint64_t));
}

This algorithm does 4 operations per bit of data (a left-shift <<, a right-shift >>, a bitwise and & and a bitwise or |), thus having a cost in O(n) where n is the size in bit of the input. Given that modern ciphers can have a cost as low as half a cycle per byte (like Chacha20 on AVX-512 for instance), spending 1 cycle per bit (8 cycles per byte) transposing the data would make bitslicing too inefficient to be used in practice. However, this transposition algorithm can be improved (as shown by Knuth [3], and explained in details by Pornin [4]) by observing that the transpose of a matrix can be reccursively written as:

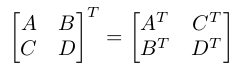
until there are only matrices of size 2x2 left (on a 64x64 matrix, this takes 6 iterations). Swapping B and C is done with shifts, ors, and ands. The key factor is that when doing this operation recursively, the same shifts/ands/ors are applied at the same time on A and B, and on C and D, thus saving a lot of operations over the naive algorithm.

As an example, let’s consider a 4x4 matrix composed of 4 4-bit data U, V, W and X. The first step is to transpose the 2x2 sub-matrices (corresponding to A, B, C and D above). Since those are 2x2 matrices, the transpition involves no reccursion:

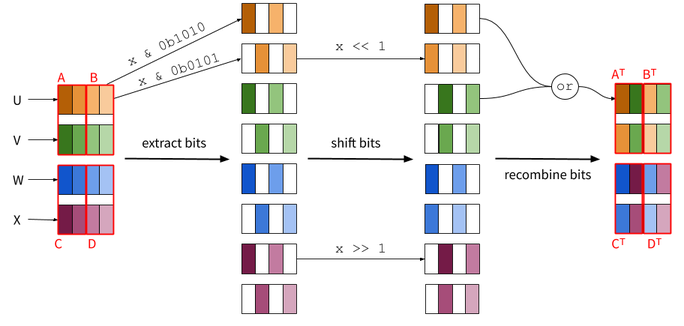
Note how transposing A and B is done with the same operations: & 0b1010 isolates the left-most bits in both A and B at the same time; << 1 shifts the right-most bits of both A and B at the same time, and the final or recombines both A and B at the same time. The same goes for C and D. B and C transposed can then be swapped in order to the finalize the whole transposition:

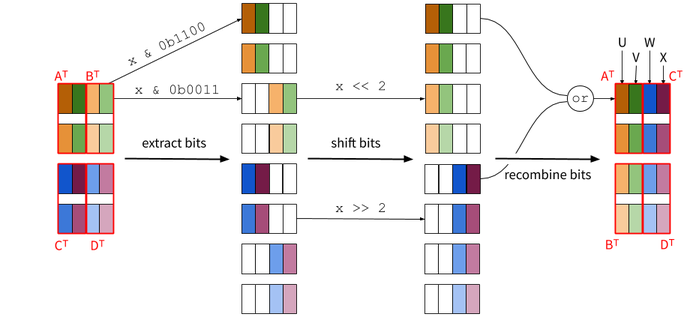
When applied to a matrix of size n x n, this algorithm does log(n) steps to get to 2x2 matrices, each of them doing n operations to swap sub-matrices B and C. The total cost is therefore O(n*log(n)) for a n x n matrix, or O(sqrt(n*log(n))) for n bits. As shown in [5], on a modern Intel computer, this amounts to 1.10 cycles per bits on a 16x16 matrix, down to 0.09 cycles per bits on a 512x512 matrix.

This algorithm allows the transposition to have a low cost when compared to the whole cipher. Furthermore, in a setting where both the encrypter and the decrypter use the same bitsliced algorithm, transposing the data can be omitted altogether. Typically, this could be the case when encrypting a hard drive.

Arithmetic operations

Bitslicing prevents from using CPU arithmetic instructions (addition, multiplication…), since each n-bit number is represented by 1 bit in n disctinct registers. Instead, bitslice programs must reimplement binary arithmetic, using bitwise instructions, like hardware manufacturers do.

For instance, an addition can be implemented in software using an adder. The simplest adder is the ripple-carry adder, which works by chaining n full adders to add two n-bit numbers. A full adder takes two 1-bit inputs (A and B) and a carry (Cin), and returns the sum of A and B (s) as well as the new carry (Cout):

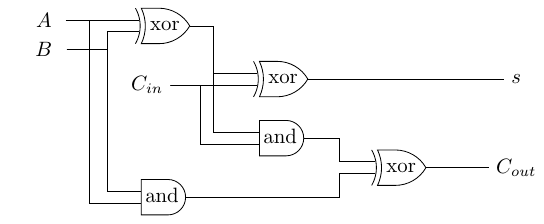
A ripple-carry adder is simply a chain of such adders:

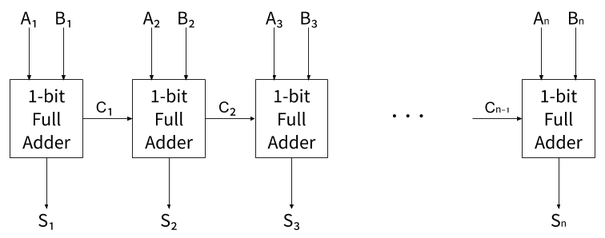
Various techniques exist to build a better hardware adders than the carry-ripple (e.g. carry-lookahead adder), but they do not apply to software, as will be detailed in a later article.

A software implementation of a n-bit carry-ripple adder thus contains n full adders, each doing 5 operations (3 xor and 2 and), for a total of 5n instructions. Since bitslicing still applies, such a code would execute m additions at once when ran on m-bit registers (e.g. 64 on 64-bit registers, 128 on SSE registers, 256 on AVX registers). The cost to do one n-bit addition is therefore 5n/m. On SSE registers, we can compare this adder with the native packed addition instructions, which do k n-bit additions with a single instruction: 16 8-bit additions, or 8 16-bit additions, or 4 32-bit additions, or 2 64-bit additions. On a Intel Skylake i5-6500, native instructions are 2 to 5 times faster than the software adder.

This slowdown by a factor of 5 could still be offset by other parts of the programs, like permutations which would be done at compile-time as mentionned above. However, implementing more complex operations like multiplication is unlikely to ever be an option for bitsliced code: while a n-bit adder requires n*5 instructions, implementing a binary multiplier requires at least n*n instructions.

Conclusion

Using bitslicing can significantly improve the throughput of a cipher, especially on CPU with SIMD extensions, which provide wide registers, enabling a lot of data-parallelism. The gains in performances however vary depending on the structure of the ciphers: permutations will be free, lookup tables will have varying performances depending on the size of the circuits needed to implement them, and arithmetic operations will always be very expensive. Furthermore, transposition often has a non-negligeable cost, making bitslicing a dubious technique for computing small circuits.

There is another issue with bitslicing: register pressure. A n-bit input is turned into n registers, but modern CPUs often only have 16 registers. Thus, a 128-bit input cannot be put into 128 registers. What will happen is a process called spilling: the data will be stored in 128 memory locations, and when some parts are actually needed, they will be loaded into registers. For instance, on a fully bitslice AES, about half the assembly instructions are move, moving data from memory to registers and back.

To overcome the cost of spilling registers, and drawing inspiration from existing adaptations of bitslicing [8], we propose a model called m-slicing, which keeps the main properties of bitslicing (constant-time, data parallelism scaling with register size), while reducing register pressure, and allowing the use of more SIMD instructions, like additions and multiplications.