Usuba - the genesis

Cryptography, from the Ancient Greek kryptos “hidden” and graphein “to write”, is the practice of securing a communication by transforming its content (the plaintext) into an unintelligible text (the ciphertext), using an algorithm called a cipher, which often takes as additional input a secret key known only from the persons encrypting and decrypting the communication. The first known use of cryptography dates back to ancient Egypt, in 1900 BCE. Almost 2000 years later, Julius Caesar was notoriously using cryptography to secure his orders to his generals, using what would later be known as a Caesar cipher, which consists in replacing each letter by another one such that the i-th letter of the alphabet is replaced by the (n+i)-th one (for some fixed n between 1 and 25), wrapping around at the end of the alphabet. Throughout history, the military would continue to use cryptography to protect their communications, with the famous example of Enigma, used by Nazi Germany during World War II. Nowadays, in our increasingly digital and ever more connected world, cryptography is omnipresent, protecting sensitive data (e.g. passwords, banking data, …) and securing data transfers over the Internet, using a multitude of ciphers.

Modern ciphers (also called cryptographic primitives) can be divided into three main categories:

• Asymmetric (or public-key) ciphers, which use two different keys for encryption and decryption: one is public and used for encryption, while the other one is private and used for decryption. Commonly used example of asymmetric ciphers include Diffie-Hellman key exchange protocol, RSA, or elliptic curves like Curve25519.

• Symmetric (or secret-key) ciphers, which use the same (secret) key for both encryption and decryption, and are sub-divided into two categories:

  • Stream ciphers, which generate a pseudo-random bit-stream and xor it with the plaintext. The most widely used stream cipher in software is Chacha20.

  • Block ciphers, which only encrypt a single fixed-size block of data at a time. When the plaintext is longer than the block length, a block cipher is turned into a stream cipher using an algorithm called a mode of operation, which describes how to repeatedly call the block cipher until the whole plaintext is encrypted. The most used block cipher is the Advanced Encryption Standard (AES) which succeeds to the now outdated Data Encryption Standard (DES).

• Hash functions, which do not require a key, and are not reversible. They are typically used to provide data integrity or to irreversibly encrypt passwords. MD5 and SHA-1 are two well-known hash functions.

While ciphers became more sophisticated, cryptanalysis, the study of breaking ciphers became more sophisticated as well. Cryptanalysis focuses on finding algorithmic weaknesses in cryptographic primitives. For instance, the Caesar cipher, presented above, is easily broken by trying to shift all letters of the ciphertext by every possible n (between 1 and 25) until it produces a text that makes sense. Examples of more advanced attacks include related-key attack [44,45,46], which consist in observing similarities in the ciphertext produced by a cipher for a given plaintext with different keys, or, similarly, differential cryptanalysis [47,48], where several plaintexts are encrypted, and the attacker tries to find statisical patterns in the produced ciphertexts. A cipher will be considered secure if no practical attacks exists, that is, no attack that can be carried out in a reasonable time or set up at a reasonable cost (e.g. billions of dollars).

Even when crytanalysis fails to break a cipher, its implementation might be vulnerable to side-channel attacks, which rely on monitoring a cipher’s execution in order to recover secret data. Side-channel attacks exploit physical vulnerabilities of the architecture a cipher is ran on: executing a cipher takes time, consumes power, induces memory transfers, etc., all of which could be attack vectors. A typical example is timing attacks [31,32,3], which exploit variations of the execution time of a cipher due to conditional branches depending on secret data. For instance, consider the following C code that checks if a provided password matches an expected password:

int check_password(char* provided, char* expected, int length) {
    for (int i = 0; i < length; i++) {
        if (provided[i] != expected[i]) {
            return 0;
        }
    }
    return 1;
}

If provided and expected start with different characters, then this function will quickly return 0. However, if provided and expected start with the same 10 characters, then this function will loop ten times (and therefore will take longer) before returning 0, thus informing an attacker monitoring the execution time of this function that he has the first characters right. This vulnerability could be fixed by decorrelating this function’s execution time from its input, making it constant-time:

int check_password(char* provided, char* expected, int length) {
    int flag = 1;
    for (int i = 0; i < length; i++) {
        if (provided[i] != expected[i]) {
            flag = 0;
        }
    }
    return flag;
}

Timing attacks can also be possible in the absence of branches on secret data: the time needed to read some data from memory on a modern Intel computer heavily depends on whether those data are in cache. An attacker could therefore design a timing attack based on cache accesses pattern, also called cache-timing attack.

More advanced, by monitoring the power consumption of a cipher rather than its timing, an attacker can use a power analysis [37, 38] to gain knowledge of secret data: power consumption can be correlated with the number of transistor switching state, which itself depends on secret data’s values [36].

Rather than being passive (i.e. observing the execution without tampering with it), an attacker can be active, and inject faults [33,34,35] in the computation (using e.g. ionizing radiations, electromagnetic impulsions, or lasers). For instance, consider the following C code, which returns some secret data if it is provided with the correct pin code:

char* get_secret_data(int pin_code) {
    if (pin_code != expected_pin_code) {
        return NULL;
    }
    return secret_data;
}

An attacker could inject a fault during this code’s execution in order to skip the return NULL instruction, which would cause this function to return the secret data even when provided with the wrong pin code.

Protecting primitive implementations requires a deep understanding of both the hardware and the existing attacks. For instance, let’s consider a function called lookup, which takes as input a 2-bit integer index, and returns the 2-bit integer at index index in an internal table table:

int lookup(int index) {
    int table[4] = { 3, 0, 1, 2 };
    return table[index];
}

This code is vulnerable to cache-timing attacks, since table[index] might hit or miss in the cache depending on index’s value. To make lookup resilient to such attacks, we can transform it to remove the table and only do constant-time bitwise operations instead:

int lookup_ct(int index) {
    // Extracting the index's 2 bits
    bool x0 = (index >> 1) & 1;
    bool x1 = index & 1;
    
    // Computing the lookup
    bool r1 = ~x1;
    bool r0 = ~(x0 ^ x1);
    
    // Recombining the result's bits together
    return (r0 << 1) | r1;
}

For instance, lookup(1) returns 0 (the value at index 1 in table). When calling lookup_ct(1), it first extracts the index’s 2 bits: the most significant bit, 0, goes into x1, and the least significant bit, 1, goes into x0. It then assigns ~x1 (0) to r1, and ~(x0 ^ x1) (0) to r0. Recombining r0 and r1 thus produces 0; like the table-based function lookup did. lookup_ct’s code does not do any memory access depending on secret data, and is thus constant-time, and therefore resilient to cache-timing attacks.

However, lookup_ct is still vulnerable to power analysis attacks: computing ~x1 for instance might consume a different amount of power depending on whether x1 is 0 or 1. To thwart power-based attacks, we can use boolean masking, which consists in representing each bit b of secret data by n random bits (called shares) such that their xor is equal to the original secret bit: b = b0 ^ b1 ^ ... ^ bn for each secret bit b. The idea being that an attacker now needs to determine the value of n bits of data in order to know the value of a single secret bit, which increases exponentially (in n) the cost of the attack. If n is greater than 2, this technique is called higher order boolean masking. Adding this protection lookup_ct would produce the following code (assuming that index has already been masked and is therefore now an array of shares):

int* lookup_ct_masked(int index[NUMBER_OF_SHARES]) {
    // Extracting the index's 2 bits
    bool x0[NUMBER_OF_SHARES], x1[NUMBER_OF_SHARES];
    for (int i = 0; i < NUMBER_OF_SHARES; i++) {
        x0[i] = (index[i] >> 1) & 1;
        x1[i] = index[i] & 1;
    }
    
    // Computing the lookup
    bool r0[NUMBER_OF_SHARES], r1[NUMBER_OF_SHARES];
    // r1 = ~x1
    r1[0] = ~x1[0];
    for (int i = 1; i < NUMBER_OF_SHARES; i++) {
        r1[i] = x1[i];
    }
    // r0 = ~(x0 ^ x1)
    r0[0] = ~(x0[0] ^ x1[0]);
    for (int i = 1; i < NUMBER_OF_SHARES; i++) {
        r0[i] = x0[i] ^ x1[i];
    }
    
    // Recombining the result's bits together
    int result[NUMBER_OF_SHARES];
    for (int i = 0; i < NUMBER_OF_SHARES; i++) {
        result[i] = (r0[i] << 1) | r1[i]
    }
    // (pretending that we can return local arrays in C)
    return result;
}

Computing a masked not only requires negating one of the shares (we arbitrarily chose the first one): negating a bit b shared as b0 and b1 is indeed (~b0) ^ b1 rather than (~b0) ^ (~b1). Computing a masked xor between two masked values on the other hand requires xoring all of their shares: (a0, a1, ..., an) ^ (b0, b1, ..., bn) = (a0^b0, a1^b1, ..., an^bn).

Protecting this code against fault injection could be done by duplicating instructions, which would add yet another layer of complexity. However, one must be careful about the interactions between countermeasures: adding protections against faults could undo some of the protections against power analysis. Even if the countermeasures do not mitigate one another, an attacker could combine fault injection and power analysis [39,40,41], which needs to be taken into account when designing countermeasures [42,43].

Applying those protection techniques to a full cipher would take a considerable amount of time and produce a very complex code.

Manually implementing high-throughput cryptographic primitives, and manually securing primitives against side-channel attacks are two complicated and tedious task, hard to get right, and which tends to obfuscate the code, thus complicating any further maintenance. Doing both at the same time is an even harder task, reaching the limits of what one can do by hand.

Instead, we propose Usuba [5,6,7], a domain-specific programming language designed to write cryptographic primitives, that I am developing as part of my PhD thesis, under the supervision of Pierre-Evariste Dagand. Usuba is a high-level programming language, making it easy to reason on programs (and therefore check their correctness). Usuba is constant-time by construction, thus protecting against cache-timing attacks, and can automatically insert countermeasures like boolean masking to protect against power-based side-channels. Finally, Usuba compiles to high-performance C code, exploiting SIMD extensions of modern CPUs when available (SSE, AVX, AVX512 on Intel, Neon on ARM, AltiVec on PowerPC), thus performing on par with hand-tuned code in a lot of cases, sometimes even better.

The design of Usuba was largely driven by the structure of blockciphers. A blockcipher is typically defined as n rounds of computation, each of them doing the same thing, and taking the output of the previous round as well as (most of the times) a key as input. The number of round is fixed for a given blockcipher, and the operations done within a round are typically bit-permutations, bitwise operations, and sometimes arithmetic operations. A blockcipher can therefore be seen as a stateless circuit. For instance, the Rectangle [13] blockcipher takes a 64-bit plaintext, and 25 64-bit keys as input, and produces the ciphertext through 24 rounds, each doing a xor, and calling two auxiliary functions: SubColumn (a lookup table), and ShiftRows (a permutation). Rectangle can therefore be represented by the following circuit:

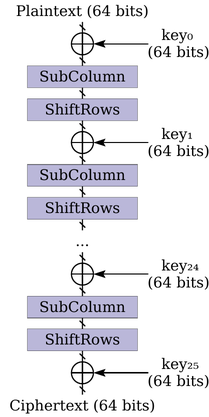
Usuba aims at providing a way to write an implementation of a cipher which is as close to the specification (i.e. the circuit) as possible. As such, Rectangle can be straight-forwardly written in Usuba in just a few lines of code (explanations below):

table SubColumn (in:v4) returns (out:v4) {
    6 , 5, 12, 10, 1, 14, 7, 9,
    11, 0, 3 , 13, 8, 15, 4, 2
}

node ShiftRows (input:u16[4]) returns (out:u16[4])
let
    out[0] = input[0];
    out[1] = input[1] <<< 1;
    out[2] = input[2] <<< 12;
    out[3] = input[3] <<< 13
tel

node Rectangle (plain:u16[4],key:u16[26][4])
       returns (cipher:u16[4])
vars round : u16[26][4]
let
    round[0] = plain;
    forall i in [0,24] {
        round[i+1] = ShiftRows(SubColumn(round[i] ^ key[i]))
    }
    cipher = round[25] ^ key[25]
tel

The code should be self explanatory: the main function Rectangle takes a plaintext as a tuple of 4 16-bit elements, and a key as a 2D array, and computes 25 rounds, each calling the functions ShiftRows, described as 3 left-rotations, and SubColumn, which computes a lookup in a table. This code is simple, and as close to the specification as can be. Yet, it compiles to a C code which is 10-15% faster than the reference implementation [6], while being much simpler and more generic, since the latter explicitly uses SSE and AVX SIMD extensions, whereas the Usuba code is not bound to a specific SIMD extension.

One of the other main benefits of Usuba is that the codes it generates are constant-time by construction. To write constant-time code with traditional languages (e.g., C) is to fight an uphill battle against compilers [22], which may silently rewrite one’s carefully crafted program into one vulnerable to timing attacks, and against the underlying architecture itself [23], whose micro-architectural features may leak secrets through timing or otherwise. For instance, the assembly generated by Clang 9.0 for the following C implementation of a multiplexer:

bool mux(bool x, bool y, bool z) {
    return (x & y) | (~x & z);
}

uses a cmove instruction, which is not specified to be constant-time (even though it seems to be, experimentally). Likewise, some integer multiplication instructions are known not to be constant-time, causing library developers to write their own software-level constant-time implementations of multiplication [25]. The issue is so far-reaching that tools traditionally applied to hardware evaluation are now used to analyze software implementations [24], treating the program and its execution environment as a single black-box and measuring whether its execution time is constant with a high enough probablity. Most modern programming languages designed for cryptography have built-in mechanism to prevent non constant-time operations. For instance, HACL* [26] has the notion of secure integers that cannot be branched on, and forbids the use of non constant-time operations like division or modulo. FaCT [27] on the other hand takes the stance that HACL* is too low-level, and that constant-timeness should be seen as a compilation problem: it provides high-level abstractions which are compiled down to constant-time idioms. Adopting yet another high-level approach, Usuba enforces constant-time by adopting (in a transparent manner from the developer’s perspective) a programming model called bitslicing.

Bitslicing was first introduced by Biham [4] as an implementation trick to speed up software implementations of DES. Intuitively, the idea of bitslicing is to represent a n-bit value as 1 bit in n registers. Each register therefore has 63-bit empty bit remaining (in the case of 64-bit registers), which can be filled in the same fashion by other independant values. To manipulate such data, the cipher must be reduced to bitwise logic operators such as x & y, x | y, x ^ y and ~ x. On a 64-bit machine, the bitwise x & y operation then effectively works like 64 parallel Boolean conjunctions, each processing a single bit. High throughput is thus achieved by parallelism: 64 instances of the cipher can execute in parallel. Bitslicing is thus especially good at exploiting vector extensions of modern CPUs, which offer large registers (e.g. 128-bit Neon on ARM, 128-bit AltiVec on PowerPC, and 128-bit SSE, 256-bit AVX and 512-bit AVX-512 on Intel). Bitsliced implementations are constant-time by design: no data-dependent conditionals nor memory accesses are made (or, in fact, possible at all). Most record-breaking software implementations of block ciphers exploit this technique [8,9,10,11], and modern ciphers are now designed with bitslicing in mind [12,13]. However, bitslicing usually implies an increase in code complexity, making it hard to write efficient bitslice code by hand, as can be demonstrate by the few lines of C code which are part of a DES implementation written by Matthew Kwan [28]:

s1 (r31 ^ k[47], r0 ^ k[11], r1 ^ k[26], r2 ^ k[3], r3 ^ k[13],
	r4 ^ k[41], &l8, &l16, &l22, &l30);
s2 (r3 ^ k[27], r4 ^ k[6], r5 ^ k[54], r6 ^ k[48], r7 ^ k[39],
	r8 ^ k[19], &l12, &l27, &l1, &l17);
s3 (r7 ^ k[53], r8 ^ k[25], r9 ^ k[33], r10 ^ k[34], r11 ^ k[17],
	r12 ^ k[5], &l23, &l15, &l29, &l5);
s4 (r11 ^ k[4], r12 ^ k[55], r13 ^ k[24], r14 ^ k[32], r15 ^ k[40],
	r16 ^ k[20], &l25, &l19, &l9, &l0);

The full code goes on like this for almost 300 lines, while the Usuba equivalent is just a few lines of codes, very similar to the Rectangle code shown above. The simplicity offered by Usuba does not come at any performance cost: both Kwan’s and Usuba’s implementations exhibit similar performances, and more generally, Usuba usually performs on par with hand-tuned code.

The bitslicing model can sometimes be too restrictive as it forbids the use of arithmetic operations, and may fail to provide the expected performances, because it usually requires more registers that hardwares provide. To overcome these issues, and drawing inspiration from Kasper & Schwabe’s byte-sliced AES [11], we propose a generalization of bitslicing that we dub m-slicing. m-slicing preserves the constant-time property of bitslicing, while using less registers, and allowing to use SIMD packed arithmetic instructions (e.g., vpaddb, vmuldp), as well as vector permutations (e.g., vpshufb) to speed up permutations. The type of slicing (bitslicing or m-slicing for various m) is controlled through Usuba’s type-system, thus not inflicting any increase in code complexity: the same code will be sliced differently depending on the data’s types.

In an era where almost all high-end CPUs have dedicated hardware to run AES, making it almost unbeatable by any software implementation of any cipher, one could wonder whether Usuba actually has a role to play in modern cryptography. However, a lot of embedded devices do not have hardware support for AES, and have stringent requirements regarding code size and power consumption, which AES cannot oblige. For such devices, lightweight ciphers [14,15,16,17] are being developed as cheap alternatives to AES, and can benefit from Usuba. Even on high-end CPUs, other ciphers are starting to compete with AES, like the Chacha family, used for instance by Google in TLS rather than AES [18], and more recently chosen by WireGuard over AES that was used by its predecessor, IPsec [19]. Usuba can help efficiently implement those ciphers, which, unlike AES, are not in Intel’s instruction set. Finally, Usuba can automatically generate countermeasures against power analysis attacks, which even software implementations of AES can benefit from [30].

References

[1] Wikipedia: Chosen-plaintext attack.

[2] Wikipedia: Related-key attack.

[3] D. J. Bernstein, Cache-timing attacks on AES, 2005.

[4] E. Biham, A fast new DES implementation in software, FSE, 1997.

[5] D. Mercadier et al, Usuba, Optimizing & Trustworthy Bitslicing Compiler, WPMVP, 2018.

[6] D. Mercadier, Pierre-Evariste Dagand, Usuba: High-Throughput and Constant-Time Ciphers, by Construction, PLDI, 2019.

[7] Github Usuba.

[8] Z. Bao et al, Bitsliced Implementations of the PRINCE, LED and RECTANGLE Block Ciphers on AVR 8-bit Microcontrollers, ICICS, 2015.

[9] M. Matsui et al, On the Power of Bitslice Implementation on Intel Core2 Processor, CHES, 2007.

[10] R. Könighofer, A Fast and Cache-Timing Resistant Implementation of the AES, CT-RSA, 2008.

[11] E. Käsper, P. Schwabe, Faster and Timing-Attack Resistant AES-GCM, CHES, 2009.

[12] R. Anderson et al, Serpent: A New Block Cipher Proposal, FSE, 1998.

[13] W. Zhang et al, RECTANGLE: A Bit-slice Lightweight Block Cipher Suitable for Multiple Platforms, 2014.

[14] S. Banik et al, GIFT: A Small Present - Towards Reaching the Limit of Lightweight Encryption, CHES, 2017.

[15] A. Baysal, S. Sahin, RoadRunneR: A Small And Fast Bitslice Block Cipher For Low Cost 8-bit Processors, LightSec, 2015.

[16] A. Bogdanov et al, PRESENT: An Ultra-Lightweight Block Cipher, CHES, 2007.

[17] V. Grosso et al, LS-Designs: Bitslice Encryption for Efficient MaskedSoftware Implementations, FSE, 2014.

[18] E. Bursztein, Speeding up and strengthening HTTPS connections for Chrome on Android, 2014, accessed 20/11/2019.

[19] J. A. Donenfeld, WireGuard: Next Generation Kernel Network Tunnel, 2019.

[20] G. Barthe, High-Assurance Cryptography: Cryptographyic Software We Can Trust, IEEE Security & Privacy, 2015.

[21] K. Bhargavan et al, Everest: Towards a Verified, Drop-in Replacement of HTTPS, SNAPL, 2017.

[22] G. Balakrishnan et al, WYSINWYX: What You See Is Not What You eXecute, VSTTE, 2005.

[23] A. Moghimi et al, MemJam: A False Dependency Attack againstConstant-Time Crypto Implementations, 2017.

[24] O. Reparaz et al, Dude, is my code constant time?, DATE, 2016.

[25] T. Pornin, Constant-time mul, accessed 12/2019.

[26] J.-K. Zinzindohoué et al, HACL*, A Verified Modern Crytographic Library, ACM Conference on Computer and Communications Security, 2017.

[27] S. Cauligi et al, FaCT: A Flexible, Constant-Time Programming Language, SecDev, 2017.

[28] M. Kwan, Bitslice DES, accessed 2019-01-04.

[29] D. J. Bernstein, Chacha, a variant of Salsa20, 2008.

[30] P. Kiaei et al, SKIVA: Flexible and Modular Side-channel and Fault Countermeasures, 2019.

[31] P. C. Kocher, Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems, CRYPTO, 1996.

[32] David Brumley, Dan Boneh, Remote timing attacks are practical, USENIX Security Symposium, 2003.

[33] E. Biham, A. Shamir, A New Cryptographic Attack on DES, 1996.

[34] F. Bao et al, Breaking public key cryptosystems on tamper resistant devices in the presence of transient faults, Security Protocols Workshop, 1997.

[35] R. Anderson, M. Kuhn, Low Cost Attacks on Tamper Resistant Devices, Security Protocols, 1997.

[36] P. Kocher et al., Introduction to differential power analysis, Cryptographic Engineering, 2011.

[37] P. Kocher et al., Differential Power Analysis, CRYPTO, 1999.

[38] T. S. Messerges, Using Second-Order Power Analysis to Attack DPA Resistant Software, CHES, 2002.

[39] F. Amiel et al., Passive and Active combined Attacks: Combining Fault Attacks and Side Channel Analysis, FDTC, 2007.

[40] T. Roche et al., Combined Fault and Side-Channel Attack on Protected Implementations of AES, CARDIS, 2011.

[41] J. Fan et al., To Infinity and Beyond: Combined Attack on ECC Using Points of Low Order, CHES, 2011.

[42] O. Reparaz et al., CAPA: The Spirit of Beaver against Physical Attacks, CRYPTO, 2018.

[43] Siemen Dhooghe, Svetla Nikova, My Gadget Just Cares For Me - How NINA Can Prove Security Against Combined Attacks, 2019.

[44] Alex Biryukov, Dmitry Khovratovich, Related-key Cryptanalysis of the Full AES-192 and AES-256, ASIACRYPT, 2009.

[45] J. Kesley et al., Related-Key Cryptanalysis of 3- WAY, Biham-DES, CAST, DES-X, NewDES, RC2, and TEA, ICICS, 1997.

[46] M. Bellare, T. Kohno, A Theoretical Treatment of Related-Key Attacks: RKA-PRPs, RKA-PRFs, and Applications, EUROCRYPT, 2003.

[47] E. Biham, A. Shamir, Differential cryptanalysis of DES-like cryptosystems, CRYPTO, 1990.

[48] X. Lai et al., Markov Ciphers and Differential Cryptanalysis, EUROCRYPT, 1991.