Usubac - front-end
Usuba’s compiler, Usubac, consists of two phases: the front-end, whose role is to distill Usuba’s high-level constructs into a minimal core language, and the back-end, which performs optimizations over the core language. The core language, called Usuba0, amounts to dataflow graphs of Boolean and arithmetic operators. In its final pass, the back-end translate Usuba0 to C code with intrinsics. The whole pipeline is shown bellow:
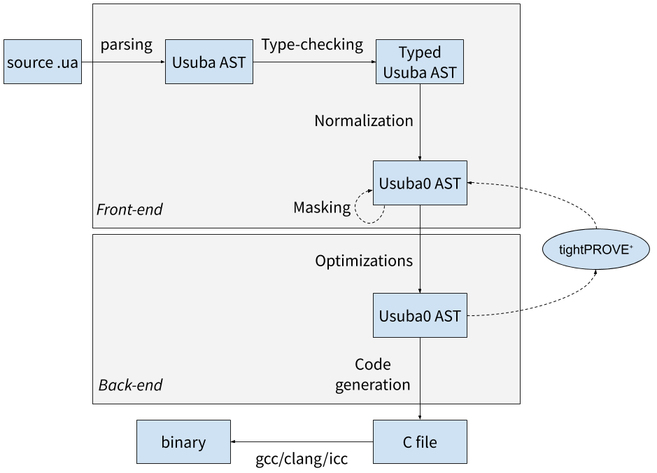
In this post, we will present the front-end. The back-end will be presented in a later post. The “Masking” and “tightPROVE+” passes add countermeasures against power-based side-channel attacks in the codes generated by Usubac. They are both optional, and will be discussed in a separate post.
The front-end extends the usual compilation pipeline of synchronous dataflow languages [1, 2], namely normalization and scheduling, with domain-specific transformations. Normalization enforces that, aside from nodes, equations are restricted to defining variables at integer type. Scheduling checks that a given set of equations is well-founded and constructively provides an ordering of equations for which a sequential execution yields a valid result. In our setting, scheduling has to be further refined to produce high-performance code: scheduling belongs to the compiler’s back-end.
Several features of Usuba requires specific treatment by the front-end. First, the language offers domain-specific syntax for specifying cryptographic constructs such as lookup tables or permutations. We boil these constructs down to Boolean circuits (see post 5 - Usuba). Second, while our vectors allow for a permissive programming discipline for developpers, they require some special transformations in order to facilitate both optimizations and generation of C. Finally, the language provides a limited form of parametric polymorphism while offering an overloading mechanism for logical and arithmetic operations based on ad-hoc polymorphism. We produce monomorphic code [7], with types and operations being expanded to machine baked instructions for the target architecture and parallelism discipline.
Vectors
Operations on vectors
As shown in post 5 - Usuba, logical and arithmetic operations applied to vectors are unfolded. For instance, the last instruction of Rectangle is:
cipher = round[25] ^ key[25]
Where cipher, round[25] and keys[25] are all of type
u16[4]. Thus, this operations is expanded by the front-end to:
cipher[0] = round[25][0] ^ key[25][0]
cipher[1] = round[25][1] ^ key[25][1]
cipher[2] = round[25][2] ^ key[25][2]
cipher[3] = round[25][3] ^ key[25][3]
Shifts and rotations involving vectors are performed by the front-end
altogether. For instance, the ShiftRows node of Rectangle contains
the following rotation:
out[1] = input[1] <<< 1;
In bitslice mode, out[1] and input[1] are both vectors of type
b1[16]. Usubac thus applies the rotation and this instruction
becomes:
out[1] = (input[1][1], input[1][2], input[1][3], input[1][4],
input[1][5], input[1][6], input[1][7], input[1][8],
input[1][9], input[1][10], input[1][11], input[1][12],
input[1][13], input[1][14], input[1][15], input[1][0])
Vector assignments
Assignments between vectors are expanded into assignments from atoms to atoms. This serves three purposes: first, Usubac will eventually generate C code, which does not support vector assignment. Second, this makes optimizations easier; in particular copy propagation and common subexpression elimination. Third, doing this before the scheduling pass (which belongs to the back-end) allows a vector assignment to be scheduled non-contiguously, which improves performances in some cases. The previous example is thus turned into:
(out[1][0], out[1][1], out[1][2], out[1][3],
out[1][4], out[1][5], out[1][6], out[1][7],
out[1][8], out[1][9], out[1][10], out[1][11],
out[1][12], out[1][13], out[1][14], out[1][15]) =
(input[1][1], input[1][2], input[1][3], input[1][4],
input[1][5], input[1][6], input[1][7], input[1][8],
input[1][9], input[1][10], input[1][11], input[1][12],
input[1][13], input[1][14], input[1][15], input[1][0])
Which is then expanded into:
out[1][0] = input[1][1];
out[1][1] = input[1][2];
out[1][2] = input[1][3];
out[1][3] = input[1][4];
out[1][4] = input[1][5];
out[1][5] = input[1][6];
out[1][6] = input[1][7];
out[1][7] = input[1][8];
out[1][8] = input[1][9];
out[1][9] = input[1][10];
out[1][10] = input[1][11];
out[1][11] = input[1][12];
out[1][12] = input[1][13];
out[1][13] = input[1][14];
out[1][14] = input[1][15];
out[1][15] = input[1][0];
Node calls
By default, all nodes of an Usuba program (except for the last one)
are inlined. Experimentally, on an Intel high-end CPU, it is never
detrimental to performances, and often beneficial. However, the
developer may want to reduce the size of the binaries generated by
Usubac; when targeting embedded devices for instance. For such cases,
a node definition can be annotated with _no_inline in order to
prevent Usubac from inlining it, or the flag -no-inline can be
passed to Usubac to disable inlining altogether. Node calls then
become function calls in the generated C code.
Usubac strives to not expand vectors in function calls in order to
reduce the overhead of pushing and popping arguments of the function
onto the stack. This is especially more important in bitslice
mode. Consider for instance, consider Rectangle’s ShiftRows, whose
bitslice signature is
node ShiftRows (input:b1[4][16]) returns (out:b1[4][16])
If input and out were to be expanded, ShiftRows would take 64
parameters as input, which would requires 64 instructions to push on
the stack, and 64 to pop. Instead, by keeping them as vectors, the
overhead of calling this function is almost negligible.
When keeping vectors non-expanded, we need to make sure that the node’s
parameters matches its provided argument. Indeed, from Usuba’s
standpoint, given a variable x of type b1[2], f(x[0],x[1]) is
equivalent to f(x). However, when generating C, those two
expressions are very different, and only one of them can be valid.
Expanding parameters and arguments
In a first pass, we make sure that every node calls has the right amount of parameters of the right types. This is done with a procedure whose pseudo-code follows:
procedure expand_params:
for each node call f(args):
for each (param,arg) in (f.params,args):
if type(param) > type(arg):
expand(arg)
restart_current_loop()
else if type(arg) > type(param):
expand(param)
restart()
else:
# do nothing
The predicate type returns the type of its argument. The comparison
> on types counts the sizes of its arguments (i.e. how many atoms
they contain), and does an integer comparison on those sizes. For
instance,
u1[2] > u1[3] === 2 > 3 === false
u1[4][2] > u1[3][3] === 8 > 9 === false
u1[6][2] > u1[8] === 12 > 8 === true
Note that since type-checking succeeded, both arguments of > are
guaranteed to have the same atomic type (i.e., if one as type u2,
the other one cannot have type u8).
expand(x) on a node parameter x expands a single level of
x. That is, if x is multi-dimentional vector, only one dimension is
expanded. For instance,
expand(x:u1[2]) = (x0:u1,x1:u1)
expand(x:u1[2][3]) = (x0:u1[3],x1:u1[3])
This requires rewriting the node’s body to take this transformation
into account: all instances of x need to be rewritten. expand on a
node call argument works in the same manner, but does not require
modifying any other statements. After expanding a parameter of a node
f, the whole procedure expand_params need to be restarted since
other calls to f which previously had the correct types could now be
wrong. For instance, consider the following Usuba program:
node f(a:b2[2]) returns (r:b2[2])
let
b = a;
tel
node g(a,b:b2) returns (r:b2[2])
let
r = f(a,b)
tel
node main(a:b2[2]) returns (r:b2[2])
vars c:b2[2]
let
c = f(a);
r = g(c);
tel
Assuming that match_params starts with main, then:
-
c = f(a)has the correct amount of parameters: one input and one output. -
r = g(c)has the correct amount of variables on the left hand-side, but only one argument in the call toginstead of two. It is thus replaced byr = g(c[0], c[1]). -
Then,
g’s body is looked at:-
r = f(a,b)has one output as expected, but two inputs instead of one.f’s parameterais thus expanded, andfbecomes:node f(a0,a1:b2) returns (r:b2[2]) let b = (a0, a1) tel -
main’s call tof(c = f(a)) is now wrong because it has only one parameter when it should have two.match_paramsthus starts again from the begining, and changes it toc = f(a[0],a[1]). No further expansion is required in the program.
-
The final program is thus:
node f(a0,a1:b2) returns (r:b2[2])
let
b = (a0,a1);
tel
node g(a,b:b2) returns (r:b2[2])
let
r = f(a,b)
tel
node main(a:b2[2]) returns (r:b2[2])
vars c:b2[2]
let
c = f(a[0],a[1]);
r = g(c[0],c[1]);
tel
Fixing dimensions
An additional pass must be done in order to make sure that node call’s
argument have the right dimensions. From Usuba’s perspective,
x:u1[2][3] and y:u1[6] can both be use interchangeably when they
are not indexed. This applies to node calls: given a node
f(x:u1[3][2]), f(x) and f(y) are both valid calls for the
type-checker, yet none can be directly translated to C. To fix node’s
parameters dimensions, we use a procedure similar to match_params:
procedure fix_dim:
for each node call f(args):
for each (param,arg) in (f.params,args):
if nesting_level(param) > nesting_level(arg):
collapse_last_dims(param)
restart()
else if nexting_level(arg) > nesting_level(param):
collapse_last_dims(arg)
restart()
else if is_same_dim(param,arg):
collapse_last_dims(param)
collapse_last_dims(arg)
restart()
else:
# do nothing
Where nesting_level returns the number of multi-dimentionality of a
vector:
nesting_level(x:u1[3]) = 1
nesting_level(x:u1[2][3][2]) = 3
nesting_level(x:u1) = 0
is_same_dim returns true if both its argument have different
dimensions. For instance,
is_same_dim(u1[6],u1[6]) = false
is_same_dim(u1[2][3],u1[3][2]) = true
is_same_dim(u1[3][2][3],u1[2][3][3]) = true
And collapse_last_dims collapses the last dimensions of a vector:
collapse_last_dims(u1[2][2]) = u1[4]
collapse_last_dims(u1[2][3][5]) = u1[2][15]
Thus, if a parameter (resp. argument) has a nesting level larger than
the provided arguments (resp. parameter), its last two dimensions are
collapsed together. This does not guarantee that it now matches with
the argument and fix_dim must therefore be iterated until a fixed
point is reached. Consider for instance a parameter of type
u1[4][2][3] and an argument of type u1[12][2]. Collapsing the last
two dimensions of u1[4][2][3] produces a
u1[4][6]. is_same_dim(u1[12][2],u1[4][6]) will return true, and
cause both types to be collapsed into mono-dimensional vectors of type
u1[24].
When collapse_last_dims is called on a parameter of a node f,
f’s body must be rewritten in order to account from the new type of
the parameter. This might cause a miss-match between the arguments of
a node call g within f and g’s arguments. For instance,
node g(x,y:u1[2]) returns (r:u1[4])
let
r = (x,y)
tel
node f(x:u1[2][2]) returns (r:u1[4])
let
r = g(x[0],x[1])
tel
node main(x:u1[4]) returns (r:u1[4])
let
r = f(x)
tel
In this program, all node calls have the right amount of
arguments. However, main is calling f with a vector of type
u1[4] whereas f expects a vector of type u1[2][2]. f’s
parameter x is thus collapsed into a vector of type u1[4] and
f becomes:
node f(x:u1[4]) returns (r:u1[4])
let
r = g(x[0],x[1],x[2],x[3])
tel
And the call to g now have more arguments than it
should. expand_params must thus be called in order to expand the
parameters of g.
Finally, the transformations done by expand_params and fix_dims
are not only necessary for nodes that are not inlined, but are also
facilitate the inlining of regular nodes. Consider for instance the
following program:
node f(a:u1[2][2]) returns (b:u1[4])
let
b[0] = a[0][0];
b[1] = a[0][1];
b[2] = a[1][0];
b[3] = a[1][1];
tel
node g(x:u1[4]) returns (y:u1[4])
let
y = f(x);
tel
In this example, when inlining f(a) in g, we would ideally like to
replace y = f(x) with f’s body with a replaced by x. However,
this requires a and x to have the same type and would thus not
work without having applied expand_params and fix_dims.
Monomorphization
The parametric polymorphism offered by Usuba enables the concise
description of size-generic or direction-generic algorithms. The
choice of execution model can thus be postponed to
compile-time. However, the code generated by Usuba must be
monomorphic. Striving for performance, we cannot afford to manipulate
boxed values at run-time. Furthermore, the underlying SIMD
architecture does not allow switching between a vertical or horizontal
style of SIMD operations. The Usubac compiler provides flags -H and
-V to monomorphize the main node to the corresponding horizontal or
vertical direction, while the -m m flag monomorphizes the atomic
word size to
the given positive integer m.
Crucially, we do not implement ad-hoc polymorphism by dictionary passing [3], which would imply a run-time overhead, but resort to static monomorphization [4]. Provided that type-checking was successful, we know precisely which operator instance exists at the given type and macro-expand it.
Flattening from m-slicing to bitslicing.
We may also want to flatten an m-sliced cipher to a purely bitsliced
model. Performance-wise, it is rarely (if ever) interesting: the
higher register pressure imposed by bitslicing is too detrimental.
However, some architectures (such as 8-bit micro-controllers) do not
offer vectorized instruction sets at all. Also, bitsliced algorithms
can serve as the basis for hardening software implementations against
fault attacks [5, 6]. To account for these use-cases, Usuba can
automatically flatten a cipher into bit-sliced form. Flattening is a
whole-program transformation (triggered by passing the flag -B to
Usubac) that globally rewrites all instances of vectorial types
u<D>m×n into the type bm[n]. Note that the vectorial direction of
the source is irrelevant: it will be collapsed after flattening. The
rest of the source code is processed as-is: we rely solely on ad-hoc
polymorphism to drive the elaboration of the operators at the
rewritten types. Either type checking (and, therefore, type-class
resolution) succeeds, in which case we have obtained the desired
bitsliced implementation, or type-class resolution fails, meaning that
the given program exploits operators that are not available in
bitsliced form. For instance, short of providing an arithmetic
instance on b8, we will not be able to bitslice an algorithm relying
on addition on u<V>8.
Once again, we rely on ad-hoc polymorphism to capture (in a single conceptual framework) the fact that a given program may or may not be amenable to bitslicing. The user is thus presented with a meaningful type error, which points out exactly which operator is incompatible with (efficient) bitslicing.
Usuba0
The front-end produces a monomorphic dataflow graph whose nodes correspond to logical and arithmetic operations provided by the target instruction set. This strict subset of the Usuba language is called Usuba0, whose grammar follows:
nd ::= (node declaration)
| node id(tv+) returns (tv+)
vars tv+
let eq+ tel
tv ::= id : typ (variable declaration)
typ ::= (type)
| typ[n] (vector)
| u<V>m (vertical atoms)
| u<H>m (horizontal atoms)
| nat (static constant)
eq ::= (equation)
| forall i in [aexpr,aexpr] { eq+ } (loop)
| var = expr (simple equation)
| var+ = f(var+) (node call)
var ::= (variable)
| x (variable)
| x[aexpr] (vector index)
expr ::= (expression)
| var (variable)
| n (constant)
| unop var (unary operation)
| var binop var (binary operation)
| var shiftop aexpr (shift)
| Shuffle(var, [n+]) (shuffle)
aexpr ::= (static arithmetic expression)
| n (constant)
| var (variable)
| aexpr binop aexpr (binary operation)
binop ::= + | - | * | & | ^ | "|"
unop ::= - | ~
shiftop ::= << | >> | <<< | >>>
Usuba0 nodes are restricted to standard nodes (i.e., no permutations nor lookup tables). Types are monomorphic atoms or vectors. Vector indices are allowed, but ranges and slices are forbidden. Expressions are not recursive, and vector assignments are not allowed except for the return values of function calls. All operators in Usuba0 map directly to machine instructions.
Usuba0 translates almost directly to C: in principle, we only need to schedule the code after which each equation turns into a variable assignment of an integer type. Nodes are translated to function definitions whereas node calls translate to function calls. However, the Usuba0 code produced by the front-end is subjected to several optimizations before delivery to a C compiler. We shall describe these transformations in the next post.
References
[1] D. Biernacki et al., Clock-directed modular code generation for synchronous data-flow languages, LCTES, 2008.
[2] F. Rocheteau, Extension du langage LUSTRE et application à la conception de circuits : le langage LUSTRE-V4 et le système POLLUX (Extension of the lustre language and application to hardware design: the lustre-v4 language and the pollux system), 1992.
[3] P. Wadler, S. Blott, How to Make ad-hoc Polymorphism Less ad-hoc, POPL, 1988.
[4] S. Kaes, Parametric Overloading in Polymorphic Programming Languages, ESOP, 1988.
[5] B. Lac et al., Thwarting Fault Attacks against Lightweight Cryptography using SIMD Instructions, ISCAS, 2018.
[6] C. Patrick, Lightweight Fault Attack Resistance in Software Using Intra-instruction Redundancy, SAC, 2016.
[7] P. Wadler, S. Blott, How to Make ad-hoc Polymorphism Less ad-hoc, POPL, 1989.