Usuba

The Usuba language design is driven by a combination of algorithmic and hardware-specific constraints: implementing a block cipher requires some discipline to achieve high throughput and avoid timing attacks.

Timing attacks can have two main causes: conditional based on secret data, and memory accesses based on secret data. The first one is not an issue for block ciphers, since they never rely on conditional based on secret data. We translate this in Usuba by simply not including a conditional operator in the language. The second cause on the other hand is nullified by the slicing Usuba relies on: both bitslicing and mslicing prevent the use of memory accesses based on conditional data.

To get high throughput, we focus exclusively on block ciphers, and assumes that they are used in a parallelizable mode (e.g. CTR). We translate this constraint by forbidding feedback loops in our designs. An Usuba program can therefore be understood as a stateless combinational circuit, parallelizable by design.

Usuba must be expressive enough to describe hardware-oriented ciphers, such as DES or Trivium, which are specified in terms of Boolean operations. For instance, the first operation of DES is defined as the following 64-bit bit-permutation applied to the plaintext:

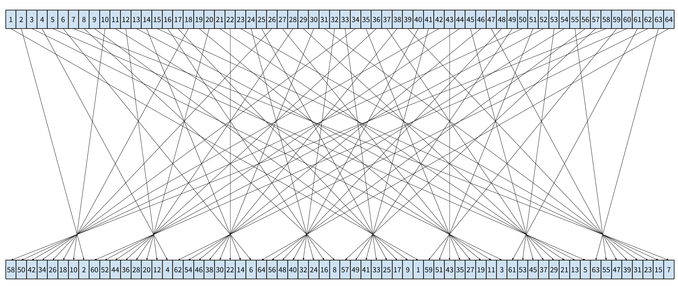
To account for such ciphers, Usuba provides abstractions to manipulate bitvectors, such as extracting a single bit as well as splitting or combining vectors.

Finally, Usuba must also be able to describe software-oriented ciphers specified in terms of affine transformations, such as AES and, more generally, ciphers exploiting maximum distance separable matrices [1]. For instance, one of AES’s underlying functions (MixColumns) multiplies the plaintext, seen as a 4x4 matrix, with a constant matrix:

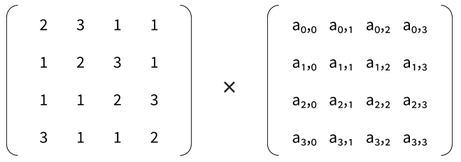
Where the a_i,j represent the 16 bytes of plaintext. To account for such ciphers, Usuba handles the matricial structure of each block of data, allowing bit-level operations to carry over such structured types while driving the compiler into generating efficient SIMD code. Altogether, Usuba provides a vector-based programming model, allowing us to work at the granularity of a single bit while providing static type-checking and compilation to efficient code.

Usuba programs are also subject to architecture-specific constraints. For instance, a cipher relying on 32-bit multiplication is but a poor candidate for bitslicing: this multiplication turns into a genuine multiplier circuit simulated in software. Similarly, a cipher relying on 6-bit arithmetic would be impossible to execute in vertical slicing: the SIMD instruction sets manipulate bytes as well as 16-bit, 32-bit and 64-bit words, leaving aside such an exotic word-size. We are therefore in a rather peculiar situation where, on the one hand, we would like to implement a cipher once, while, on the other hand, the validity of our program depends on a combination of slicing mode and target architecture.

How can we, at compile time, provide meaningful feedback to the Usuba programmer so as to (always) generate high-throughput code? We address this issue by introducing a type for structured blocks (Section Data Layout) upon which we develop a language (Section Syntax & Semantics) supporting parametric polymorphism (for genericity) and ad-hoc polymorphism (for architecture-specific code generation) as well as a type system (Section Type System) ensuring that “well-typed programs do always vectorize”.

Data Layout

Our basic unit of computation is the block, i.e. a bitvector of statically-known length. To account for its matricial structure and its intended parallelization, we introduce the type u<D>m×n to denote n ∈ ℕ* registers of unsigned m-bit words (m ∈ ℕ* and “u” stands for “unsigned”) that we intend to parallelize using vertical (D = V) or horizontal (D = H) SIMD instructions. A single m-bit value is thus typed u<D>m×1, abbreviated u<D>m. This notation allows us to unambiguously specify the data layout of the blocks processed by the cipher. Consider the 64-bit input block of the Rectangle cipher:

Bitsliced Rectangle manipulates blocks of type u<‘D>1×64, i.e. each bit is dispatched to an individual register:

A 16-bit vertical slicing implementation of Rectangle manipulates blocks of type u<V>16×4, i.e. each one of the 4 sub-blocks is dispatched to the first 16-bit element of 4 registers:

The double vertical lines represent the end of each 16-bit packed elements. Horizontally sliced Rectangle has type u<H>16×4, i.e. each 16-bit word is horizontally spread across each of the 16 packed elements of 4 SIMD registers:

Note that directions collapse in the case of bitslicing, i.e. u<V>1×64 ≅ u<H>1×64. Both cases amount to the same layout, or put otherwise: vertical and horizontal slicing are two generalizations of bitslicing.

For a given data layout, throughput is maximized by filling the remaining bits (in grey on the figures) of the registers with subsequent blocks of the input stream, following the same pattern. Thus, a vertical, 16-bit SIMD addition (e.g. vpaddw on AVX) in vertical slicing will amount to performing an addition on 8 blocks in parallel. We emphasize that the types merely describe the structure of the blocks, and do not specify the parallelization strategy, nor the architecture to be used. An Usuba program thus only specifies the treatment of a single slice, from which Usuba’s compiler automatically generates code to maximize register usage. Transposing a sequence of input blocks in a form suitable for parallel processing is thus fully determined by its type.

Syntax & Semantics

In and of itself, Usuba is an unsurprising dataflow language [3, 4]. We use the example of Rectangle to illustrate Usuba’s syntax and semantics:

table SubColumn (in:v4) returns (out:v4) {
    6 , 5, 12, 10, 1, 14, 7, 9,
    11, 0, 3 , 13, 8, 15, 4, 2
}

node ShiftRows (input:u16[4]) returns (out:u16[4])
let
    out[0] = input[0];
    out[1] = input[1] <<< 1;
    out[2] = input[2] <<< 12;
    out[3] = input[3] <<< 13
tel

node Rectangle (plain:u16[4],key:u16[26][4])
       returns (cipher:u16[4])
vars round : u16[26][4]
let
    round[0] = plain;
    forall i in [0,24] {
        round[i+1] = ShiftRows(SubColumn(round[i] ^ key[i]))
    }
    cipher = round[25] ^ key[25]
tel

In the following, we shall leave types and typing aside, coming back to this point in the next section.

Nodes

An Usuba program is composed of a totally ordered set of nodes (SubColumn, ShiftRows and Rectangle in the case of Rectangle). The last node plays the role of the main entry point: it will be compiled to a C function. The compiler is left free to compile internal nodes to functions or to inline them. A node typically consists of an unordered system of equations involving logic and arithmetic operators. The semantics is defined extensionally as a solution to the system of equations, i.e. an assignment of variables to values such that all the equations hold.

Usuba also provides syntactic sugar for declaring lookup tables, useful for specifying S-boxes. Rectangle’s S-box can thus be written as:

table SubColumn (in:v4) returns (out:v4) {
    6 , 5, 12, 10, 1, 14, 7, 9,
    11, 0, 3 , 13, 8, 15, 4, 2
}

Conceptually, a lookup table is an array: a n-bit input indexes into an array of 2ⁿ possible output values. However, to maximize throughput and avoid cache timing attacks, the compiler expands lookup tables to Boolean circuits. For prototyping purposes, Usuba uses an elementary logic synthesis algorithm based on binary decision diagrams (BDD) –inspired by [5]– to perform this expansion. The circuits generated by this tool are hardly optimal: finding optimal representations of S-boxes is a full time occupation for cryptographers, often involving months of exhaustive search [6, 7, 8, 9]. Usuba integrates these hard-won results into a database of known circuits, which is searched before trying to convert any lookup table to a circuit. For instance, Rectangle’s S-box (SubColumn) is replaced by the compiler with the following node:

node SubColumn (a:v4) returns (b:v4)
  vars t1,t2,t3,t4,t5,t6,t7,t8,t9,t10,t11,t12 : v1
  let 
    t1   = ~a[1]; 
    t2   = a[0] & t1; 
    t3   = a[2] ^ a[3];
    b[0] = t2 ^ t3; 
    t5   = a[3] | t1; 
    t6   = a[0] ^ t5; 
    b[1] = a[2] ^ t6; 
    t8   = a[1] ^ a[2]; 
    t9   = t3 & t6; 
    b[3] = t8 ^ t9; 
    t11  = b[0] | t8; 
    b[2] = t6 ^ t11
tel

Bit-permutations are commonly used in cryptographic algorithm to provide diffusion. Usuba offers syntactic support for declaring bit-permutations. For instance, the initial permutation of DES mentioned in the introduction of this post amounts to the following declaration specifying which bit of the input bitvector should be routed to the corresponding position of the output bitvector:

perm init_p (a:b64) returns ( out:b64 ) {
     58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4,
     62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8,
     57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3,
     61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7
}

It should be read as “the 1^st bit of the output is the 58^th bit of the input, the 2^nd bit of the output is the 50^th of the input, etc.”. The direct bitsliced translation of this permutation is a function of 64 Boolean inputs and 64 Boolean outputs, which consists of simple assignments: out[0] = a[58]; out[1] = a[50]; ... After Usuba’s copy propagation pass, a bit-permutation is thus no more than a (static) renaming of variables.

Finally, usuba also offers a way to define an array of nodes, tables or permutations. For instance, the Serpent cipher uses a different S-box for each round, all of which can be grouped into the same array of tables:

table[] sbox(input:v4) returns (out:v4) [
    { 3, 8,15, 1,10, 6, 5,11,14,13, 4, 2, 7, 0, 9,12 } ;
    {15,12, 2, 7, 9, 0, 5,10, 1,11,14, 8, 6,13, 3, 4 } ;
    { 8, 6, 7, 9, 3,12,10,15,13, 1,14, 4, 0,11, 5, 2 } ;
    { 0,15,11, 8,12, 9, 6, 3,13, 1, 2, 4,10, 7, 5,14 } ;
    { 1,15, 8, 3,12, 0,11, 6, 2, 5, 4,10, 9,14, 7,13 } ;
    {15, 5, 2,11, 4,10, 9,12, 0, 3,14, 8,13, 6, 7, 1 } ;
    { 7, 2,12, 5, 8, 4, 6,11,14, 9, 1,15,13, 3,10, 0 } ;
    { 1,13,15, 0,14, 8, 2,11, 7, 4,12,10, 9, 3, 5, 6 }
]

Those S-boxes can then be called using the following syntax:

x = sbox<3>(y)

The 3 can be replaced by any arithmetic expression. Arrays of nodes/tables/permutations are especially useful to be used in forall loops (introduced below). For instance, Serpent’s main forall loop contains:

sbox<i%8>(...)

To call the i^th S-box at the i^th round (modulo 8).

Vectors

Syntactically, our treatment of vectors stems from the work on hardware synthesis of synchronous dataflow programs [10]. Given a vector x of size n (thus, of type τ[n]), we can obtain the element x[k] at position 0 ≤ k < n and the consecutive elements x[k..l] in the range 0 ≤ k < l < n. This syntax is instrumental for writing concise bit-twiddling code. Indices must be known at compile-time, since variable indices could compromise the constant-time property of the code. The type-checker can therefore prevent out-of-bounds accesses. Noticeably, vectors are maintained in a flattened form. Given two vectors x and y of size, respectively, m and n, the variable z = (x, y) is itself a vector of size m+n (not a pair of vectors). Conversely, for a vector u of size m+n, the equation (x, y) = u stands for x = u[0..n] and y = u[n..m + n].

Loops

To account for repetitive definitions (such as the wiring of the 25 rounds of Rectangle), the forall construct lets us declare a group of equations within static bounds. Its semantics is intuitively defined by macro-expansion: we can always translate it into a chunk of inter-dependent equations. However, in practice, Usuba’s compiler preserves this structure in its pipeline and may generate imperative loops performing destructive updates. Serpent’s main loop for instance is:

forall i in [0,30] {
    state[i+1] = linear_layer(sbox<i%8>(state[i] ^ keys[i]))
}

Each of the 31 iteration computes a round of Serpent: it xors the result of the previous round (state[i]) with the key for this round (keys[i]), then calls the S-box for this round (sbox<i%8>), and finally calls the node linear_layer and stores the result in state[i+1] for the next round. Since this loop relies on calling an array of tables, and the notion of array of functions does not exists in C, Usubac compiler has no choice but to fully unroll it.

Imperative assignment

Some ciphers (e.g. Chacha20, Serpent) are defined in an imperative manner, repetitively updating a local state. Writing those ciphers in a synchronous dataflow language can be tedious: it amounts to writing code in static single assignment (SSA) form. To simplify such codes, Usuba provides an assignment operator x := e (where x may appear free in e). It desugars into a standard equation with a fresh variable on the left-hand side that is substituted for the updated state in later equations. For instance, Serpent’s linear layer can be written as:

node linear_layer(x:u32x4) returns (out:u32x4)
let
    x[0] := x[0] <<< 13;
    x[2] := x[2] <<< 3;
    x[1] := x[1] ^ x[0] ^ x[2];
    x[3] := x[3] ^ x[2] ^ (x[0] << 3);
    x[1] := x[1] <<< 1;
    x[3] := x[3] <<< 7;
    x[0] := x[0] ^ x[1] ^ x[3];
    x[2] := x[2] ^ x[3] ^ (x[1] << 7);
    x[0] := x[0] <<< 5;
    x[2] := x[2] <<< 22;
    out = x
tel

Which desugars to:

node linear_layer(x:u32x4) returns (out:u32x4)
vars t0, t1, t2, t3, t4, t5, t6, t7, t8, t9: u32
let
    t0 = x[0] <<< 13;
    t1 = x[2] <<< 3;
    t2 = x[1] ^ t0 ^ t1;
    t3 = x[3] ^ t1 ^ (t0 << 3);
    t4 = t2 <<< 1;
    t5 = t3 <<< 7;
    t6 = t0 ^ t4 ^ t5;
    t7 = t1 ^ t5 ^ (t4 << 7);
    t8 = t6 <<< 5;
    t9 = t7 <<< 22;
    out = (t8, t9, t4, t5);
tel

Operators

The constructs introduced so far deal with the wiring and structure of the dataflow graph. To compute, one must introduce operators. Usuba supports bitwise logical operators (conjunction &, disjunction |, exclusive-or ^ and negation ~), arithmetic operators (addition +, multiplication * and subtraction -), shifts of vectors (left << and right >>), rotations of vectors (left <<< and right >>>), and intra-register bit shuffling (Shuffle). Their availability and exact implementation (especially, run-time cost) depend on the slicing mode and the target architecture, as shown next.

Type System

Base types

For the purpose of interacting with its cryptoraphic runtime, the interface of a block cipher is specified in terms of the matricial type u<D>m×n, which documents the layout of blocks coming in and out of the cipher. We also have general vectors whose types are τ[n], for any type τ. Now, consider the subkeys used by vsliced Rectangle: they are presented as an object key of type u<V>16×4[26], which is 26 quadruples of 16-bit words. To obtain the key at round 23, we thus write key[23]. To obtain the 3rd word of that key, we write key[23][3]. The notation u<D>m×4[26] indicates that accesses must be performed in column-major order, i.e. as if we were accessing an object of type u<D>m[26][4] (following C convention). In fact, because vectors are kept flat, the types u<D>m[26][4] and u<D>m×4[26] are actually equivalent from the typechecker’s standpoint. This apparent redundancy is explained by the fact that types serve two purposes. In the surface language, matricial types (u<D>m×4) document the data layout and its SIMDization. In the target language, the matricial structure is irrelevant: an object of type u<D>m×4[26] supports exactly the same operations as an object of type u<D>m[26][4]. Surface types are thus normalized, after type-checking, into distilled types. A value of type u<D>m×1 (for all D) is called an atom, and its type is said to be atomic.

Parametric polymorphism.

A final addition to our language of types is the notion of parametric word size and parametric direction. A cipher like Rectangle can in fact be sliced horizontally or vertically: both modes of operation are compatible with the various SIMD architectures introduced after SSSE3. Similarly, the node SubColumn amounts to a Boolean circuit whose operations (&, |, ^, and ~) are defined for any atomic word size (ranging from a single Boolean to a 512-bit AVX512 register): SubColumn thus applies to u<D>1, u<D>8, etc. This completes the grammar of distilled types, including type parameters in word size and direction:

n ∈ ℕ (integers)

⟨τ⟩ ::= (types)
  | u<D>⟨m⟩ (base type)
  | τ[n] (vectors)
  | nat (static constants)

⟨m⟩ ::= (size)
  | ‘m (parameter)
  | n (fixed size)

⟨D⟩ ::= (direction)
  | ‘D (parameter)
  | V (vertical)
  | B (horizontal)

Nodes being first-order functions, a function type is (at most) rank-1 polymorphic: the polymorphic parameters it may depend on are universally quantified over the whole type (and node body). We use the abbreviation bn (n bits) and um (unsigned integer of size m) for the type u<‘D>1×n and, respectively, u<‘D>m×1 where ‘D is the direction parameter in the nearest scope. Similarly, we write vn for u<‘D>‘m×n when ‘m is the nearest word size parameter.

Ad-hoc polymorphism

In reality, few programs are defined for any word size or any direction. Only Boolean circuits are direction polymorphic, bitwise logical operations applying uniformly. Also, no program is absolutely parametric in the word size: we can only compute up to the register size of the underlying architecture.

To capture these invariants, we introduce a form of bounded polymorphism through type-classes [11]. Whether a given cipher can be implemented over a collection of word size and/or direction is determined by the availability of logical and arithmetic operators. We therefore introduce four type-classes for logical, arithmetic, shift/rotate and shuffle operations:

Logic(τ) :          Arith(τ) :             Shift(τ) :
 & : τ → τ → τ        + : τ → τ → τ            >> : τ → nat → τ
 | : τ → τ → τ        * : τ → τ → τ            << : τ → nat → τ
 ^ : τ → τ → τ        - : τ → τ → τ           >>> : τ → nat → τ
 ~ : τ → τ                                    <<< : τ → nat → τ
 
Shuffle(τ) :
 Shuffle:  τ → nat list → τ

The implementation of these classes depend on the type considered and the target architecture. For instance, arithmetic on 13-bit words is impossible, even in vertical mode. The generated code also depends on a combination of types and target architecture. For instance, shifting a vector amounts to renaming registers whereas shifting in horizontal mode requires an actual shuffle instruction. We chose to provide instances solely for operations that can be implemented statically or with a handful of instructions, with the exceptions of Shuffle, which is made available in vertical mode despite its cost. Our type-class mechanism is not user-extensible. The list of all the possible type-classes instances is summarized in the following table. This set of instances is obviously non-overlapping so our overloading mechanism is coherent: if the type-checker succeeds in finding an instance for the target architecture, then that instance is unique.

Both logical and arithmetic operators can be applied to a vector of size n, in which case they amount to n element-wise applications of the operator on each element of the vector. Shifting an vector on the other hand is performed at the granularity of the element on vectors, and amounts to statically renaming variables and shifting in zeros. For instance, if we consider a vector x of type b1[4], x << 2 is equivalent to (x[0], x[1], x[2], x[3]) << 2, which is reduced at compile time to (x[2], x[3], 0, 0) (with the last two 0 being of type b1).

Logic instructions can be applied on any non-vector type for any slicing, as long as the architecture offers large enough registers. Arithmetic instructions on non-vector types is only valid for vslicing, and require some support from the underlying architecture. In pratice, SSE, AVX, AVX2 and AVX512 offer instructions to do 8-bit, 16-bit, 32-bit and 64-bit arithmetics. Vertical shifts of 16-bit, 32-bit and 64-bit values use CPU shift instructions (vpsrl and vpsll on AVX2, shr and shl on general purpose x86). Shifts in horizontal slicing are compiled using shuffle instructions (vpshufd, vpshufb, etc.). For instance, consider a variable x of type u16: shifting right this variable by 2 is done using the shuffle pattern [-1,-1,15,14,13,12,11,10,9,8,7,6,5,4,3,2] (-1 in the pattern causes a 0 to be introduced). SIMD registers older than AVX512 only offer shuffles for up to 16 elements, while AVX512 does also provide 32 and 64 elements shuffle, thus allowing us to compile 64-bit shifts. Shuffle instruction in horizontal mode map naturally to SIMD shuffle instructions. And finally, Shuffle instructions in vertical mode are compiled to shifts moving each bit in a register. For instance, shuffling a variable x of type u8 with the pattern [5,2,0,1,7,6,4,3] produces the following code:

((x << 5) & 128) ^
((x << 1) & 64)  ^
((x >> 2) & 32)  ^
((x >> 2) & 16)  ^
((x >> 3) & 8)   ^
((x << 1) & 4)   ^
((x >> 2) & 2)   ^
((x >> 4) & 1)

Since SIMD instructions do not offer 8-bit shifts, 8-bit shuffles in vertical mode are only available on x86-64. Shuffles of 16, 32 and 64 bits can, on the other hand, be compiled for SIMD architectures. Shuffles are expensive in vertical mode, but we chose to support them nonetheless since some commonly used ciphers rely on them, like AES.

References

[1] S. Duval, G. Leurent, MDS Matrices with Lightweight Circuits, IACR Trans. Symmetric Cryptol. 2018.

[2] K. E. Iverson, Notation as a Tool of Thought, Commun. ACM 23, 1980.

[3] IEEE Standard VHDL Language Reference Manual, 2000.

[4] P. Caspi et al., LUSTRE: A declarative language for programming synchronous systems, POPL, 1987.

[5] T. Pornin, Constant-time mul, accessed 12/2019.

[6] D. Canright, A Very Compact S-Box for AES, CHES, 2005.

[7] M. Kwan, Reducing the Gate Count of Bitslice DES, 2000.

[8] D. A. Osvik, Speeding up Serpent, AES Candidate Conference, 2000.

[9] M. Ullrich et al., Finding optimal bitsliced implementations of 4×4-bit S-boxes, SKEW, 2011.

[10] F. Rocheteau, Extension du langage LUSTRE et application à la conception de circuits : le langage LUSTRE-V4 et le système POLLUX (Extension of the lustre language and application to hardware design: the lustre-v4 language and the pollux system), 1992.

[11] P. Wadler, S. Blott, How to Make ad-hoc Polymorphism Less ad-hoc, POPL, 1988.