Interleaving
The back-end exclusively manipulates Usuba0 code, taking advantage of
referential transparency (any variable x in an expression can be
replaced by its definition) as well as the fact that we are dealing
with a non Turing-complete language (our programs are thus very
static: loop bounds are known at compile-time, there are no
conditionals…). Optimizations carried out at this level are easier
to write but also more precise. The back-end’s optimizations are
complementary with the optimizations offered by C compilers. There is
a significant semantic gap between the user intents expressed in Usuba
and their straightforward sliced translations in C. This results in
missed optimization opportunities for the C compiler, of which we
shall study a few examples in the following. The back-end
authoritatively performs these optimizations at the level of Usuba0.
A first optimization consists in interleaving several executions of the program. Usuba allows us to systematize this folklore programming trick, popularized by Matsui [1]: for a cipher using a small number of registers (for example, strictly below 8 general-purpose registers on Intel), we can increase its instruction-level parallelism (ILP) by interleaving several copies of a single cipher, each manipulating its own independent set of variables.
This can be understood as a static form of hyper-threading, by which we (statically) interleave the instruction stream of several parallel execution of a single cipher. By increasing ILP, we reduce the impact of data hazards in the deeply pipelined CPU architecture we are targeting. Note that this technique is orthogonal from slicing (which exploits spatial parallelism, in the registers) by exploiting temporal parallelism, i.e. the fact that a modern CPU can dispatch multiple, independent instructions to its parallel execution units. This technique naturally fits within our parallel programming framework: we can implement it by a straightforward Usuba0-to-Usuba0 translation.
Example
Rectangle’s S-box for instance can be written in C using the following macro:
#define sbox_circuit(a0,a1,a2,a3) { \
int t0, t1, t2; \
t0 = ~a1; \
t1 = a2 ^ a3; \
t2 = a3 | t0; \
t2 = a0 ^ t2; \
a0 = a0 & t0; \
a0 = a0 ^ t1; \
t0 = a1 ^ a2; \
a1 = a2 ^ t2; \
a3 = t1 & t2; \
a3 = t0 ^ a3; \
t0 = a0 | t0; \
a2 = t2 ^ t0; \
}
This implementation modifies its input (a0, a1, a2 and a3)
in-place, and uses 3 temporary variables t0, t1 and t2. It
contains 12 instructions, and we might therefore expect that it
executes in 3 cycles on a Skylake, saturating the 4 bitwise ports of
this CPU. However, it contains a lot of data dependencies: t2 = a3 |
t0 needs to wait to t0 = ~a1 to be computed; t2 = a0 ^ t2 needs
to wait for t2 = a3 | t0; a0 = a0 ^ t1 needs to wait for a0 = a0
& t0, and so on. Compiled with Clang 7.0.0, this codes executes in
about about 5.24 cycles. By interleaving two instances of this code,
the impact of data hazards is reduced:
#define sbox_circuit_interleaved(a0,a1,a2,a3,a0_2,a1_2,a2_2,a3_2) { \
int t0, t1, t2; int t0_2, t1_2, t2_2; \
t0 = ~a1; t0_2 = ~a1_2; \
t1 = a2 ^ a3; t1_2 = a2_2 ^ a3_2; \
t2 = a3 | t0; t2_2 = a3_2 | t0_2; \
t2 = a0 ^ t2; t2_2 = a0_2 ^ t2_2; \
a0 = a0 & t0; a0_2 = a0_2 & t0_2; \
a0 = a0 ^ t1; a0_2 = a0_2 ^ t1_2; \
t0 = a1 ^ a2; t0_2 = a1_2 ^ a2_2; \
a1 = a2 ^ t2; a1_2 = a2_2 ^ t2_2; \
a3 = t1 & t2; a3_2 = t1_2 & t2_2; \
a3 = t0 ^ a3; a3_2 = t0_2 ^ a3_2; \
t0 = a0 | t0; t0_2 = a0_2 | t0_2; \
a2 = t2 ^ t0; a2_2 = t2_2 ^ t0_2; \
}
This code contains twice the S-box code (visually separated to make it
clearer): one implementation computes the S-box on a0, a1, a2
and a3 while the other computes it on a second input, a0_2,
a1_2, a2_2 and a3_2. This code runs in 7 cycles; or 3.5 cycles
per S-box, which is much closer to the ideal 3 cycles/S-box. We shall
call it 2-interleaved.
Despite the interleaving, some data dependencies remain, and it may be
tempting to interleave a third execution of the S-box. However, since
each S-box requires 7 registers (4 for the input, and 3 temporaries),
this would require 21 registers, and only 16 general purpose register
are available on Intel. Still, we benchmarked this 3-interleaved
S-box, and it executes 12.92 cycles, or 4.3 cycles/S-box; which is
slower than the 2-interleaved one, but still faster than without
interleaving at all. Inspecting the assembly code reveals that in the
3-interleaved S-box, 4 values are spilled, thus requiring 8 additional
move operations (4 stores and 4 loads). The 2-interleaved S-box does
not contain any spilling.
Remark. In order to benchmark the S-box, we put it in a loop that
we unrolled 10 times (using Clang’s unroll pragma). This unrolling
is required because of the expected port saturation: if the S-box
without interleaving was to use ports 0, 1, 5 and 6 of the CPU for 3
cycles, this would leave no free port to perform the jump at the end
of the loop. In practice, since the non-interleaved S-box does not
saturate the ports, this does not impact performance. However,
unrolling improves performance of the 2-interleaved S-box –which puts
more pressure on the execution ports– by 14%.
Initial benchmark
To benchmark our interleaving optimization, we considered 10 ciphers with low register pressure, making them good candidates for interleaving. We started by generating non-interleaved and 2-interleaved implementations on general purpose registers for Intel. We compiled the generated codes with Clang 7.0.0. The results are shown in the following table (sorted by instructions per cycle):
| Cipher | Instructions per cycle | Speedup | |
|---|---|---|---|
| without interleaving | with 2-interleaving | ||
| xoodoo | 3.92 | 3.79 | 0.85 |
| clyde | 3.89 | 3.93 | 0.97 |
| gimli | 3.82 | 3.86 | 0.87 |
| gift | 3.57 | 3.54 | 0.94 |
| chacha20 | 3.55 | 3.95 | 0.95 |
| pyjamask | 3.36 | 3.49 | 1.07 |
| ace | 2.90 | 3.69 | 1.23 |
| ascon | 2.89 | 3.30 | 1.15 |
| serpent | 2.65 | 3.60 | 1.35 |
| rectangle | 2.61 | 3.40 | 1.25 |
Interleaving is more beneficial on ciphers with low instructions per cycle (IPC). In all cases, the reason for the low IPC is data hazards. The 2-interleaved implementations reduce the impact of those data hazards, and bring the IPC up while increasing performance. We will examine each case one by one in the next section.
Factor and granularity
We now know that interleaving can indeed increase performances of ciphers suffering from tight dependencies.Our interleaving algorithm is parametrized by a factor and a granularity. The factor determines the number of implementations to be interleaved, while the granularity describes how the implementations are interleaved: 1 instruction from an implementation followed by 1 from another one would be a granularity of 1, while 5 instructions from an implementation followed by 5 from another one would be a granularity of 5. For instance, the Rectangle 2-interleaved S-box above has a factor of 2 and a granularity of 1 since instructions from the first and the second S-box are interleaved one by one. A granularity of 2 would be the following code:
t0 = ~a1; \
t1 = a2 ^ a3; \
t0_2 = ~a1_2; \
t1_2 = a2_2 ^ a3_2; \
t2 = a3 | t0; \
t2 = a0 ^ t2; \
t2_2 = a3_2 | t0_2; \
t2_2 = a0_2 ^ t2_2; \
a0 = a0 & t0; \
a0 = a0 ^ t1; \
a0_2 = a0_2 & t0_2; \
a0_2 = a0_2 ^ t1_2; \
t0 = a1 ^ a2; \
a1 = a2 ^ t2; \
t0_2 = a1_2 ^ a2_2; \
a1_2 = a2_2 ^ t2_2; \
And a granularity of 4 would be:
t0 = ~a1; \
t1 = a2 ^ a3; \
t2 = a3 | t0; \
t2 = a0 ^ t2; \
t0_2 = ~a1_2; \
t1_2 = a2_2 ^ a3_2; \
t2_2 = a3_2 | t0_2; \
t2_2 = a0_2 ^ t2_2; \
a0 = a0 & t0; \
a0 = a0 ^ t1; \
t0 = a1 ^ a2; \
a1 = a2 ^ t2; \
a0_2 = a0_2 & t0_2; \
a0_2 = a0_2 ^ t1_2; \
t0_2 = a1_2 ^ a2_2; \
a1_2 = a2_2 ^ t2_2; \
The user can use the flags -inter-factor <n> and -inter-granul <n>
to instruct Usubac to generate a code using a given interleaving
factor and granularity.
The granularity is only up to a function call or loop, since we do not duplicate function calls but rather the arguments in a function call. The rational being that interleaving is supposed to reduce pipeline stalls within functions (resp. loops), and duplicating function calls (resp. loops) would fail to achieve this. For instance, the following Usuba code (extracted from our Chacha20 implementation):
state[0,4,8,12] := QR(state[0,4,8,12]);
state[1,5,9,13] := QR(state[1,5,9,13]);
state[2,6,10,14] := QR(state[2,6,10,14]);
is 2-interleaved as (with QR’s definition being modified
accordingly):
(state[0,4,8,12],state_2[0,4,8,12]) := QR_x2(state[0,4,8,12],state_2[0,4,8,12]);
(state[1,5,9,13],state_2[1,5,9,13]) := QR_x2(state[1,5,9,13],state_2[1,5,9,13]);
(state[2,6,10,14],state_2[2,6,10,14]) := QR_x2(state[2,6,10,14],state_2[2,6,10,14]);
Rather than:
state[0,4,8,12] := QR(state[0,4,8,12]);
state_2[0,4,8,12] := QR(state_2[0,4,8,12]);
state[1,5,9,13] := QR(state[1,5,9,13]);
state_2[0,4,8,12] := QR(state_2[0,4,8,12]);
state[2,6,10,14] := QR(state[2,6,10,14]);
state_2[0,4,8,12] := QR(state_2[0,4,8,12]);
Note that interleaving is done after inlining and unrolling in the pipeline, which means that any node call still present in the Usuba0 code will not be inlined.
To evaluate how the factor and the granularity impact performance, we
generated implementations of 10 ciphers with different factors (0
(without interleaving), 2, 3, 4 and 5), and different granularities
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20, 30, 50, 100, 200). We used
Usubac’s -unroll and -inline-all flags to fully unroll and inline
the codes (this flags will be discussed in a later post) in order to
eliminate the impact of loops and function calls from our
experiment. Overall, we generated 19.5 millions of lines of C code in
700 files for this benchmark.
We benchmarked our interleaved implementations on general purpose registers rather than SIMD ones, and verified that the front-end was not a bottleneck. SIMD assembly instructions are larger than general purpose ones. Since most codes (eg. HPC applications) on SIMD are made of loops and function calls, decoded instructions are stored in the instruction cache (DSB). However, since we fully inlined and unrolled the codes, the legacy pipeline (MITE) is used to decode the instructions, and can only process up to 16 bytes of instruction per cycle. AVX instructions can easily take 7 bytes (an addition where one of the operand is a memory address for instance), and 16 bytes often correspond to only 2 instructions; not enough to fill the pipeline.
We report the results in the form of graphs showing the throughput (in cycles per bytes; lower is better) of each cipher depending on the interleaving granularity for each interleaving factor.
Remark. When benchmarking interleaving on general purpose
registers, we were careful to disable Clang’s auto-vectorization
(using -fno-slp-vectorize -fno-vectorize). Failing to do so produces
inconsistent results since Clang erratically and partially vectorizes
some implementations and not others. Furthermore, we would not be
benchmarking general purpose registers anymore since the vectorized
code would use SSE or AVX registers.
Ace

One of Ace’s basic block is a function that computes ((x <<< 5) & x)
^ (x <<< 1). It contains 4 instructions, and yet cannot be done in
less than 3 cycles, because of its inner dependencies. Interleaving
this function twice means that it contains 8 instructions which cannot
execute in less than 3 cycles, wasting 4 port-cycle. Interleaving it 3
times or more allows it to fully sature its ports (i.e. run its 12
instructions in 3 cycles), and it is indeed slightly faster (less than
2 percents though) than the 2-interleaved implementation despite
containing more spilling, and is 1.25x faster than the non-interleaved
implementation.
Ace also contains other idioms that can limit CPU utilization, like
0xfffffffe ^ ((rc >> i) & 1), which also cannot execute in less than
3 cycles despite containing only 3 instructions. Those idioms benefit
from interleaving as well.
Interleaving 4 or 5 times introduces some spilling which reduces performance, but minimizes the impact of data hazard enough to be better than the non-interleaved implementation. For comparison, the 5-interleaved implementation does 27 times more reads/stores to/from memory than the non-interleaved one and is still 1.16x faster.
In all cases, the granularity has a low impact. The reordering done by Clang, as well as the out-of-order nature of the CPU are able to schedule the instructions in a way to reduce the impact of data hazards. When the granularity is too coarse (100 and 200 instructions), performance start to decrease.
Rectangle
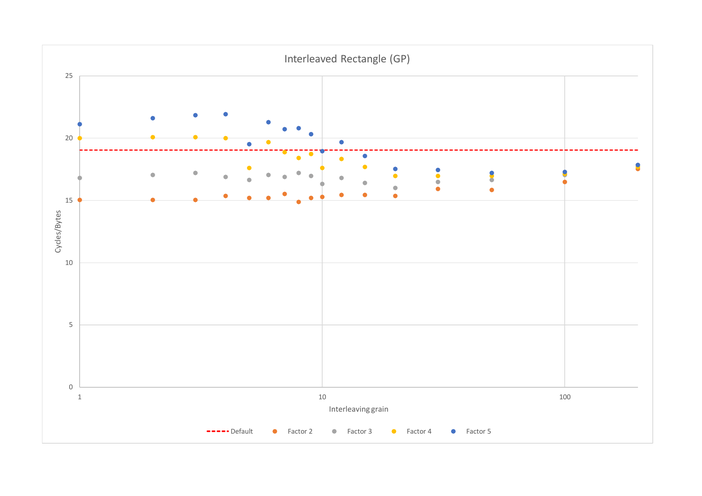
We have already shown Rectangle’s S-box in this post’s introduction. It contains 12 instructions, and could be executed in 4 cycles if it wasn’t slowed down by data-dependencies: its run time is actually 5.24 cycles. Interleaving 2 (resp. 3) times Rectangle gives a speedup of x1.26 (resp. x1.13), regardless of the granularity. The number of loads and stores in the 2-interleaved Rectangle implementation is exactly twice the number of loads and stores in the non-interleaved implementation: interleaving introduced no spilling at all. On the other hand, the 3-interleaved implementation suffers from spilling and thus contains 4 times more memory operations than the non-interleaved one, which results in slower performance than the 2-interleaved version.
Interleaving 4 or 5 instances with a small granularity (less than 10) introduces too much spilling which reduces performance. Increasing granularity reduces spilling while still allowing the C compiler to schedule the instructions in a way to reduce the impact of data hazards. For instance, 5-interleaved Rectangle with a granularity of 50 contains twice less memory loads and stores than with a granularity of 2: temporary variables from all 5 implementations tend not to be alive at the same time when the granularity is large enough, while they are when the granularity is small.
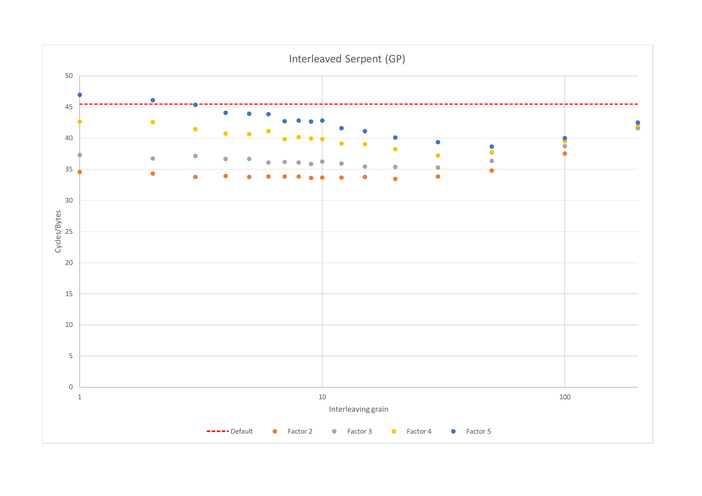
Serpent
Serpent only requires 5 registers (4 for the state and 1 temporary
register used in the S-box). Its linear layer contains 28 instructions
xors and shifts, yet executes in 14 cycles due to data
dependencies. Likewise, the S-boxes were optimized by Osvik [2] to put
a very low pressure on the registers, and to exploit a superscalar CPU
that is able to execute only two bitwise instructions per cycle
(whereas modern Intel CPUs can do 3 or 4 bitwise instructions per
cycles). For instance, the first S-box contains 17 instructions, but
executes in 8 cycles. This choice made sense back when there were only
8 general purpose registers available, among which one was reserved
for the stack pointer, and one was use to keep a pointer to the key,
leaving only 6 registers available.
Now that we have 16 registers available, interleaving several implementations of Serpent makes sense and does greatly improve performances as can be seen from the graph. Once again, interleaving more than two implementation introduces spilling, and does not improve performances.
On AVX however, all 16 registers are available for use: the stack pointer and the pointer to the key are kept in general purpose registers rather than AVX ones. 3-interleaving therefore introduces less spilling than on GP registers, making it 1.05 times faster than 2-interleaving:
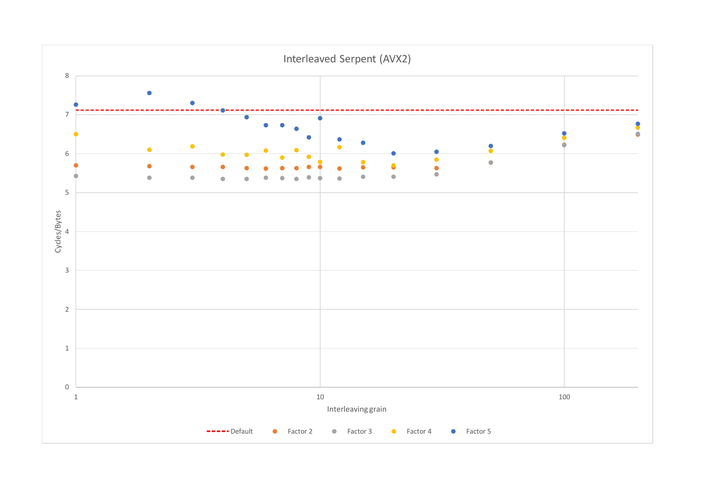
The current best AVX2 implementation of Serpent is -to the best of our knowledge- the one from the Linux kernel, written by Kivilinna [3], which uses 2-interleaving. Kivilinna mentions that he experimentally came to the conclusion that interleaving at a granularity of 8 is optimal for the S-boxes and that 10 or 11 is optimal for the linear layer. Using Usuba, we are able to systemize this experimental approach and we observe that, with Clang, granularity has a very low impact on performance.
Ascon

Ascon is the trickiest of the ciphers we considered when it comes to analyzing its interleaved performances. Its S-box contains 22 instructions with few enough data dependencies to allow it to run in about 6 cycles, which is very close to saturate the CPU. Its linear layer however is the following:
node LinearLayer(state:u64x5) returns (stateR:u64x5)
let
stateR[0] = state[0] ^ (state[0] >>> 19) ^ (state[0] >>> 28);
stateR[1] = state[1] ^ (state[1] >>> 61) ^ (state[1] >>> 39);
stateR[2] = state[2] ^ (state[2] >>> 1) ^ (state[2] >>> 6);
stateR[3] = state[3] ^ (state[3] >>> 10) ^ (state[3] >>> 17);
stateR[4] = state[4] ^ (state[4] >>> 7) ^ (state[4] >>> 41);
tel
This linear layer is not bottlenecked on data-dependencies, but by the
rotations: general purpose rotations can only be executed on ports 0
and 6. Only two rotations can be executed each cycle, and this code
can therefore not be executed in less than 7 cycles: 5 cycles for all
the rotations, followed by two additional cycles to finish computing
stateR[4] from the result of the rotations, each computing a single
xor.
There are two ways that Ascon can benefit from interleaving. First, if
the linear layer is executed two (resp. three) times simultaneously,
the last 2 extra cycles computing a single xor now computed two
(resp. three) xors each, thus saving one (resp. two) cycle. Second,
out-of-order execution can allow the S-box of one instance of Ascon to
execute while the linear layer of the other copy executes, thus
allowing a full saturation of the CPU despite the rotations being only
able to use ports 0 and 6.
To understand how interleaving impacts performances, we used Linux’s
perf tool to get the IPC, numbers of loads and stores, and the
number of cycles where 1, 2, 3 or 4 instructions are executed:
| Interleaving | Cycles/Bytes | IPC | #Loads/Stores (normalized) |
% of cycles where at least n µops are executed | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| none | 4.85 | 2.75 | 1 | 99.2 | 92.6 | 48.9 | 15.5 |
| x2 | 4.01 | 3.29 | 2.07 | 99.9 | 99.6 | 72.7 | 35.6 |
| x3 | 3.92 | 3.80 | 9.69 | 99.7 | 98.7 | 91.3 | 63.9 |
| x4 | 4.05 | 3.50 | 10.05 | 99.7 | 97.0 | 79.6 | 51.3 |
| x5 | 4.13 | 3.37 | 10.63 | 99.9 | 96.7 | 74.1 | 43.7 |
The non-interleaved code has a fairly low IPC of 2.75, and uses less than 3 ports on half the cycles. Interleaving twice Ascon increases the IPC to 3.29, and doubles the number of memory operations which indicates that no spilling has been introduced. However, only 72% of the cycles use 3 cycles or more, which is still no very high. 3-interleaved Ascon suffers from a lot more spilling: it contains about 10 times more memory operations than without interleaving. However, it also brings the IPC up to 3.80, and uses 3 ports or more on 91% of the cycles.
However, interleaving a fourth or a fifth copy of Ascon does not increase performances further, which is not surprising since 3-interleaved Ascon already almost saturates the CPU ports. Furthermore, 4 and 5-interleaved Ascon even reduces the port usage, because of the added memory operations (due to spilling) that bottleneck the computation.
Pyjamask
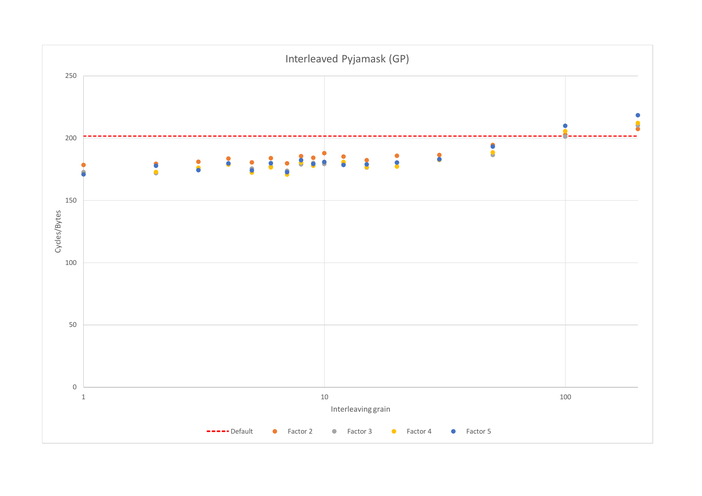
The linear layer of Pyjamask multiplies each of the 4 32-bit of the state by a 32x32 binary matrix. This operation is done bit by bit, and, for each bit, 4 operations are needed; each of them depending on the previous one. This means that for the whole matrix multiplication, which makes up most of Pyjamask, only one instruction is executed per cycle.
On general purpose registers, interleaving twice Pyjamask increases performances 1.13 times, mainly thanks to the parallelism it allows in this matrix multiplication. However, it is still not enough to fully utilize the pipeline, which is why interleaving 3, 4 or 5 times is more beneficial, despite the additional spilling it introduces.
This effect is even more noticeable on AVX registers, as can be seen in the following table:
| Interleaving | Cycles/Bytes | IPC | #Loads/Stores (normalized) |
|---|---|---|---|
| none | 54.13 | 2.71 | 1 |
| x2 | 47.18 | 2.94 | 2.83 |
| x3 | 41.35 | 3.38 | 9.8 |
| x4 | 41.91 | 3.36 | 26.3 |
| x5 | 42.67 | 3.50 | 67 |
Interleaving twice increases performances by x1.18, while interleaving three times increases performances by 1.31x, depsite increasing the amount of memory operations by 9.8 (and therefore the amount of memory operations per input by 3.3). Even the 5-interleaved version is more efficient than the non-interleaved one, despite containing 66 times more loads and stores.
Another factor explaining the speedup offered by interleaving on Pyjamask is the fact that the matrix used in the matrix multiplication is circular, and can therefore be computed at runtime using a simple rotation. This matrix is the same for all interleaved copies of the cipher, and the rotations can therefore be done only once for all of them.
Other ciphers
On the other ciphers we benchmarked (Chacha20, Clyde, Gift, Gimli, Xoodoo), interleaving made performances worse, as can be seen from the graphs below. As shown in Section “Initial benchmark”, all of those ciphers have very high IPC, above 3.5. None of those cipher is bound by data dependencies (except for Chacha20, on which we will come back in the post about scheduling), and the main impact of interleaving is to introduce spilling.
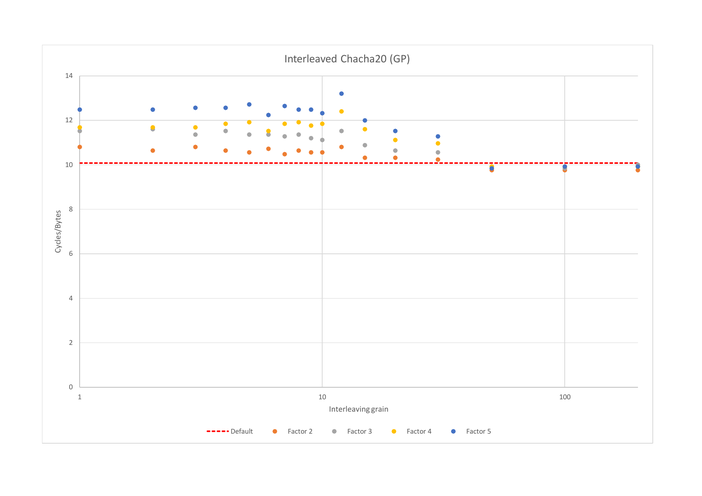

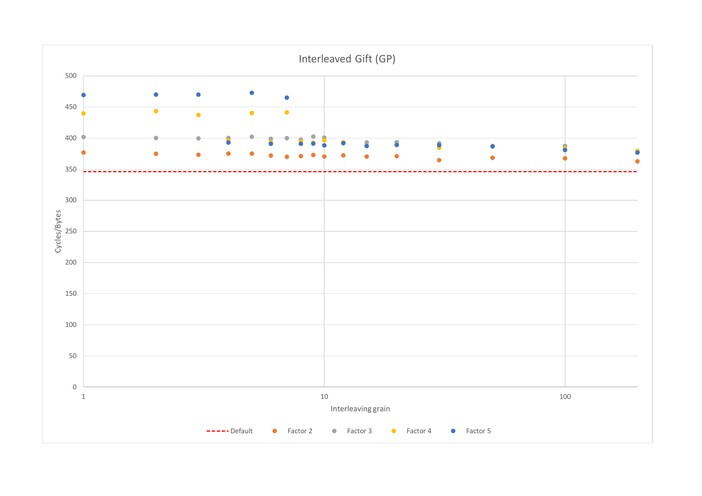
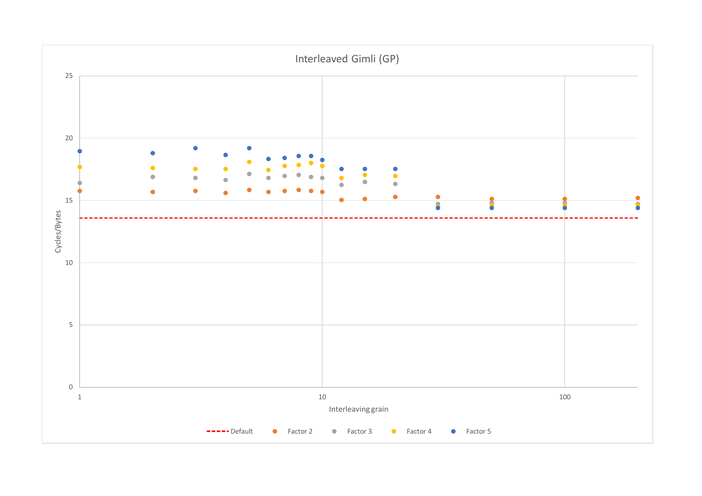

Overall impact of factor and granularity
All of the examples we considered show that choosing a coarse granularity (50 instructions or more) reduces the impact of interleaving, regardless of whether it was positive or negative. Most of the times, the granularity has little to no impact on the performances, as long as it is below 20. There are a few exceptions, which can be attributed to either compiler or CPU effects, and can be witnessed on Clyde, Gift, and Xoodoo. For instance, on Xoodoo 3-interleaved, granularities of 12 and 20 are 1.26 times than granularities of 10, 15 and 30. When monitoring the programs, we observe that implementations with a granularity of 10, 15 and 30 do 1.53 more memory accesses than the ones with a granularity of 12 and 20, thus showing that our optimizations always risk to be nullified by poor choices from the C compiler’s heuristics.
Determining the ideal interleaving factor for a given cipher is a complex task because it depends both on register pressure and data dependencies. In some cases, like Pyjamask, introducing some spilling in order to reduce the amount of data hazards is worth it, while in other cases, like Rectangle, spilling deteriorates performance. Furthermore, while we can compute the maximum number of live variables in an Usuba0 program, the C compiler is free to schedule the generated C code how it sees fit, potentially reducing or increasing the amount of live variables.
Fortunately, Usubac’s autotuner fully automates the interleaving transformation, thus releaving programmers from the burden of determining by hand the optimal interleaving parameters. When ran with the autotuner enabled, Usubac automatically benchmarks several interleaving factors (0, 2, 3 and 4) in order to find out which is best.
We do not benchmark the granularity when selecting the ideal interleaving setup, since its influence on performances is minimal. Furthermore, our scheduling algorithm (which will be presented in a later post) strives to minimize the impact of data dependencies and thus reduces even further the influence of the granularity.
References
[1] M. Matsui, How Far Can We Go on the x64 Processors?, FSE, 2006.
[2] D. A. Osvik, Speeding up Serpent, AES Candidate Conference, 2000.
[3] J. Kivilinna, Block Ciphers: Fast Implementations on x86-64 Architecture, 2013.